GALLERY 3
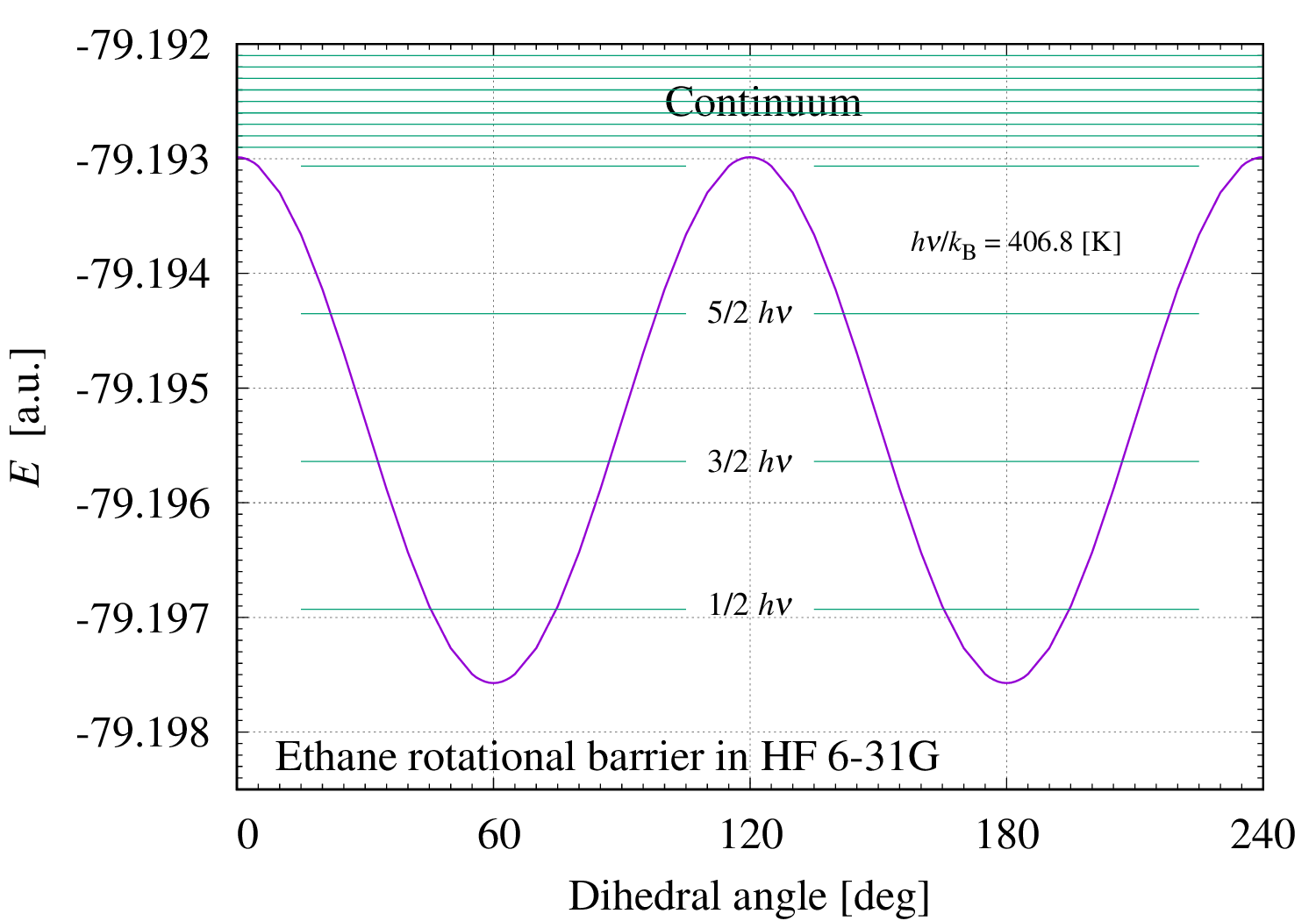
エタンの回転障壁
エタン C2H6 分子の回転障壁を求めてみた。 回転と言っても、C-C 軸を中心に2つのメチル基が回転する分子内の回転で、広義には分子振動に分類される。 この内部回転な分子振動は下の Mode 1 で見ることができる。 サムネイルは二面角(dihedral angle)を変えながら計算して得られた C2H6 のエネルギーをプロットしたものである。 計算には Hartree-Fock 理論と 6-31G 基底系を使った。二面角以外の構造は最安定構造に固定している。 グラフを見ると、二面角が 60 [deg], 180 [deg], 300 [deg] のねじれた(Staggered)構造でエネルギーが最低になり、 0 [deg], 120 [deg], 240 [deg] の重なった(Eclipsed)構造でエネルギーが最高になるのが判る。 これは C-C 軸を挟んだ水素どうしの反発と理解する事ができる。つまり、水素原子核の周囲にある電子分布どうしの重なりが小さい程、エネルギーが低くなっている。
安定構造で振動解析を行うと、励起エネルギー最小の振動モードとして内部回転が得られる。 その振動準位をグラフに重ねた。調和近似の結果に非調和性の補正(因子0.9029を掛ける)を施している。 この振動モードの波数は 283 [cm-1] (補正済み)で、励起エネルギーは 0.035 [eV] となり、温度にすると 407 [K] である。 障壁の高さを考えると、最低エネルギー構造それぞれに、2個ないし3個の離散励起状態があると予想される。これに加えて二面角が回っている連続状態がある。 二面角 60 [deg] の基底状態を反応物、隣の 180 [deg] または -60 [deg] を生成物と考えると、 活性化エネルギーは約 0.004 [a.u.] ≈ 0.1 [eV] ≈ 10 [kJ/mol] になる。 化学反応に疎い私はこの大きさに対する感覚を持ち合わせていないのだが、少し調べた所に依ると、常温ではそれなりの速さになる様だ。 つまり、常温においてエタンの二面角は一定ではなく時々飛び移っていると言う事。エタンの場合は飛び移っても前と同じですが。 とにかく、エタンの基準振動モードの内の1つはこの様に特殊なので、分子振動を考慮して比熱を計算する時には特別な取扱いが必要になる。 ちなみに、温度ゼロではトンネル効果で隣の最安定構造に移るが、物理学ではこの様な時間変化(Kink 解)をインスタントン(Instanton)と呼んでいる。 一瞬だけ現れて消える粒子があると考える。素粒子物理学には幾つかの例があるが、化学が扱う分子にもインスタントンがあった。面白い。
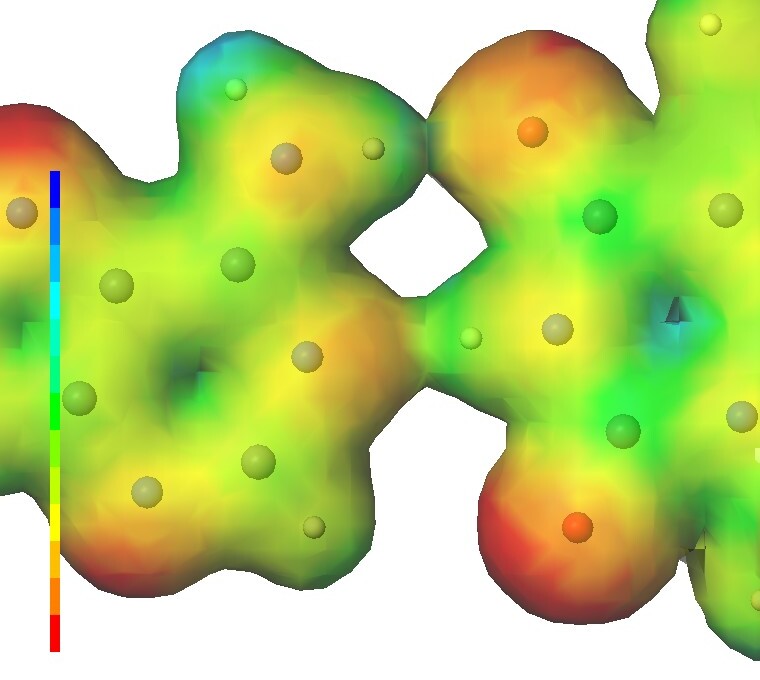
陽子の量子性と突然変異
DNA を構成しているヌクレオチド1対(2個)分を B3LYP3 密度汎関数理論と 6-31G** 基底系を使って解いてみた。 サムネイルは、アデニンとチミンが水素結合している部分の拡大図である。 静電ポテンシャルマップを透過させている。中に浮いている球を原子核だと考えよう。 もちろん、実際はもっと小さいが、実際の大きさにすると見えなくなるので大きく描いていると思って欲しい。 すると、水素結合部分にある白い球は水素の原子核つまり陽子である。 さて、細胞が分裂する前には、DNA の2本鎖が開き、そこに相補的な核酸塩基を持つヌクレオチドが結合して、DNA は2本に複製される。 つまり、DNA の複製の際には中の全ての塩基対が一旦は解離する。 では、この図の塩基対が解離するとき、水素結合部分にある陽子はどちら側に行くのだろうか?
量子化学では原子核を古典的に扱う。すなわち、電子状態を解くときには止めておいて、求まった電子分布から決まる力を原子核に加える。 しかし、実際は原子核も原子や分子というミクロの世界にある、さらに小さな粒子であり、運動は量子力学に支配されている。 特に陽子は小さいので、陽子の量子性は無視できない事が判っている。 この例で言うと、上の陽子に関しては右の酸素原子核に近い位置にも準安定な位置があり、その位置での発見確率(存在確率)も無視できない。 下の陽子も同様に左の窒素原子核に近い準安定位置での発見確率も無視できない。 従って、上の問いの答えは、すなわち陽子の行き先は、1通りではない。 この例では、高い確率で上の陽子は左のアデニン側に下の陽子は右のチミン側に行くが、その他の行き方も起こり得るのである。 その他のなかでは特に、上の陽子が右に行ってかつ下の陽子が左に行く、互変異性体と呼ばれる変異が起こるとの事。 確率的には最も起きそうにないが、塩基中の水素の数を保存しない変異は何らかの理由で抑制あるいは排除されるのだろう。
ここで困った事に、変異したアデニンはチミンではなくシトシンと結合し、変異したチミンはアデニンではなくグアニンと結合するのだそうだ。 つまり、DNA 複製中に互変異性体が発生すると、元とは塩基配列が異なった DNA が生成される。つまり、DNA の複製ミス、突然変異が発生する。 これを知って、「生物の進化も量子力学に起源があった!」と喜びたいところだが、 「量子力学で生命の謎を解く」 に依れば、陽子の量子性が実際の生物の進化に寄与した事を示す証拠はまだないとの事である(DNA の突然変異は放射線などの様々な外的な要因によっても起きる)。 残念。でも、確かな証拠を押さえるのが難しいだけで、実際は寄与したと考えて良いだろう。今後の進展に期待したい。
上の本の著者たちは、適応的突然変異と呼ばれる受け入れ難い実験結果は、陽子の量子性で説明できると考えている。 要するに、変化した環境に適した突然変異は、量子的な意味で環境変化の前から DNA に存在しており(全ての塩基対で正常体と互変異性体の状態が重なっており)、 実際に環境が変化したときに自然選択で適応的な変異が定着する、と言うのだ。 例えるなら、生命が量子コンピュータを使っていた、になろうか。事実なら非常に面白い。 上で「困った事に」と書いた性質も、この目的の為に功名に仕組まれていたのだろうか?だとしたら出来過ぎで恐ろしい。
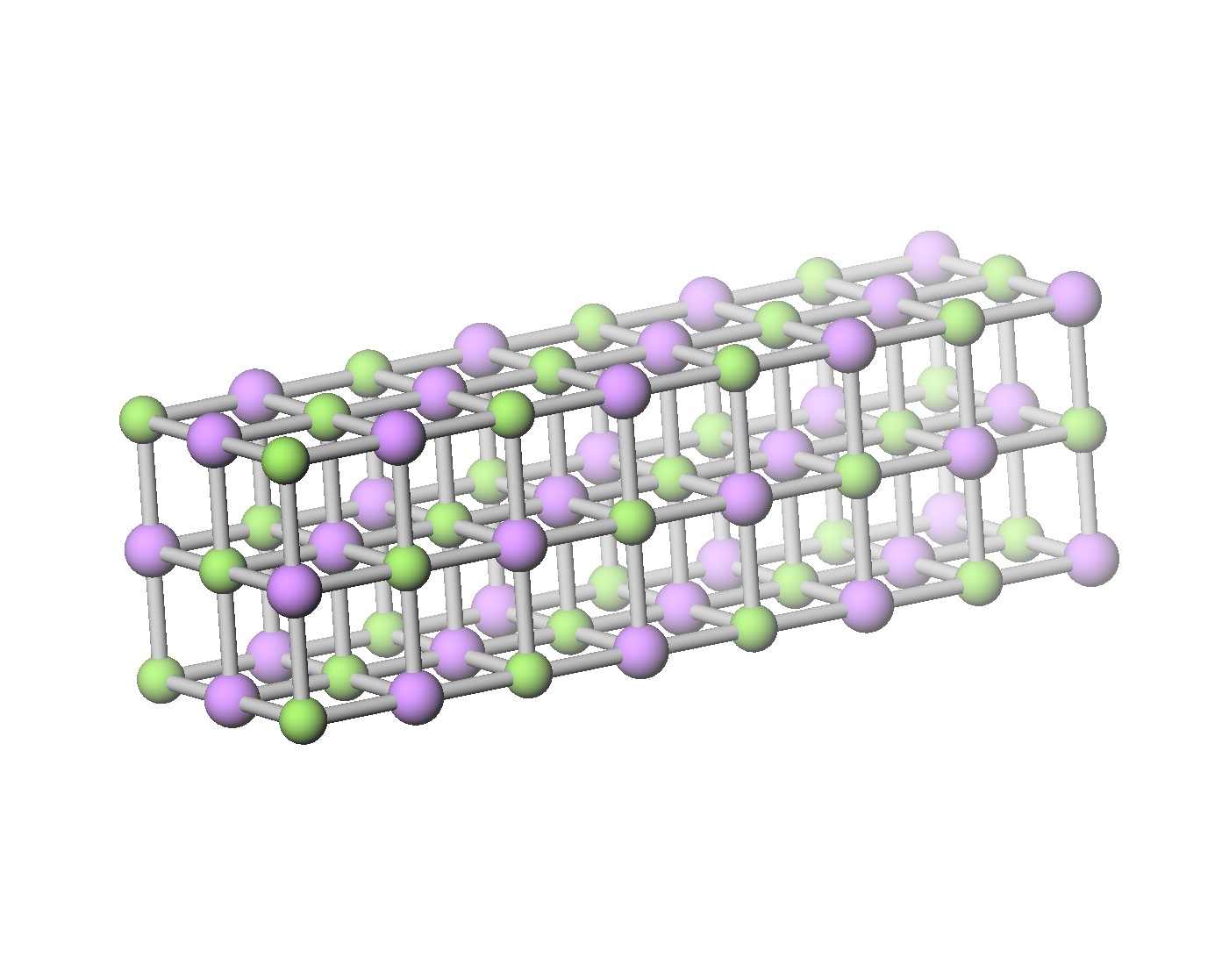
イオン結晶と無限級数
サムネイルは以前にも載せたフッ化リチウムの結晶の模型である。 現実世界の結晶は、これが3次元方向にくり返し繋がって大きな結晶になっている。 そのくり返しの回数は 1020 のオーダーなので、無限にくり返されていると扱うのはごく自然である。 実際、結晶中の電子状態を求めるときや、溶融塩を動力学計算するときには、箱に周期境界条件を課して無限系にする。
さて、結晶中のあるイオンが他のイオンから受け取る静電(ポテンシャル)エネルギーについて考えてみよう。 結晶中のある Li+ イオン(緑の球)は、結晶中の他の Li+ イオンからクーロン反発力を受けている。 この反発力のポテンシャルエネルギーを、結晶中の他の全ての相手 Li+ イオンについて合計すると、発散してしまう。 その理由はイオンが一様に分布していると近似すると分かり易い1。 全ての相手 Li+ からの静電エネルギーの合計を求めるには、 ある距離からの静電エネルギーにその距離にいるイオンの数を掛けて、それを距離に関して和を取れば良い。 クーロン力のポテンシャルエネルギーは電荷(イオン)間の距離に反比例する。つまり、距離が倍に離れると半分になる。 一方、ある距離にいる相手の数は、分布が一様の場合はその距離を半径とする球面の面積に比例しているが、 球面の面積は半径の2乗で大きくなるから、その距離にいる相手の数は距離の2乗で増えていく。 よって、掛け算の結果は距離に比例して大きくなり、無限に続く結晶を考えると、静電エネルギーの合計はいくらでも大きくなる。 つまり、プラス無限大に発散している2。 数学の言葉で言うと、静電エネルギーの合計を計算する和は単調増加の無限級数になっているから発散する3。 この発散は、 F- イオン(紫の球)が結晶中の他の全ての F- イオンから受け取る静電エネルギー合計でも同じである。 また、ある Li+ イオンが結晶中の全ての F- イオンから受け取る静電エネルギー合計は、クーロン力が引力な事に対応して、マイナス無限大に発散している。
ここまでは同種イオンのみから、あるいは異種イオンのみからを考えたが、実際の結晶中のイオンは同種イオンからも異種イオンからも静電エネルギーを受け取る。 では、その合計はいくらになるのだろうか?上で考えた様に、同種イオンからと異種イオンからとを別々に考えて足そうとすると、プラス無限大+マイナス無限大になって答えは得られない。 では、分けないで同時に和を取ったら、つまり1つの無限級数で計算したらどうだろうか?実は、その1つにした無限級数も厄介な無限級数になっている。 上で分けて計算してプラス無限大+マイナス無限大になってしまった様に、足す順番を変える事で、収束させない事も、任意の値に収束させる事も可能な級数なのである。 数学ではこの様な級数を条件収束な無限級数と呼ぶ。性質の悪い級数である。 無理やりにでも級数の結果を求めるには、足す順番の条件を付け加えなければならない。そこで、とりあえず、距離の近い順に和をとって見よう。 まず、ある Li+ イオンから一番近いのは、軸方向の隣にある F- イオンで、その数は6個。 その次に近いのは、2つの軸で作る面内の対角方向にある Li+ イオンで、その数は12個。 その次に近いのは、立方体の対角方向にある F- イオンで、その数は8個。こうやって考えて級数を作ると、 Li+-F- 間の距離を単位として、級数は
となる。しかし、残念ながらこの足し算の順番だと無限級数は収束しない。上で見た様に後ろの項で絶対値がゼロに行かず、部分和は永遠に振動してしまうのだ。 次に、別の条件として、注目する Li+ イオンを含む軸に沿った立方体を考えてその中で和を取り、その立方体大きくしていく足し方を試して見よう。 このとき、注目するイオンが立方体の端にならない様に、そのイオンを中心に対称的に立方体を広げる。辺の長さは偶数になる。1辺のイオンの数は中央の1つから2づつ大きくなるので奇数になる。 まず、辺の長さが2の1番小さな立方体を考えると、部分和は上にある距離の近い順の最初の3項の和になり、 −2.13352 と求まる。 次に大きな立方体は辺の長さ4で、前の立方体に隣接する異種イオン48個と同種イオン50個が加わって、部分和は −1.51665 と求まる。 その次は辺の長さ6で部分和は −1.91250 と求まる。 この様に立方体を大きくしていく足し算の順番だと級数はめでたく収束して、結果は −1.747565 になる4。 これで、ある1つの条件の下で条件収束な無限級数を計算できた。
さて、この様に条件を課してなんとか計算した条件収束な無限級数の結果であるが、 元々の物理的な意味は、結晶中の1つのイオンが他の全てのイオンから受け取る静電エネルギーであった。 この静電エネルギーは結晶の持つ物理化学的性質と関係しており、マイナスを外してマーデルング定数と呼ばれている。 もちろん実験で測る事もできる。そして、上でどうにか求めた計算結果 1.747565 は、実験で測った結果と良く一致しているのだ。 条件収束な無限級数の1つの収束値に過ぎない値が物質の性質を再現すると聞いて、素直な人は「奇跡!神秘!」と感動するかも知れない。 数学に強い人は「そんなバカな!」と動転するかも知れない。その通り。これにはトリックがある。
なぜ無限級数が出て来たかと言うと、結晶を構成するイオンの数があまりに多いので無限個と扱ったからだ。 つまり、ここでの無限は数学的な意味での無限ではなく非常に大きい有限なのだ。 つまり、マーデルング定数が無限級数になったのはモデル化のせいであり、正しくは(厳密には)項数が有限な級数である。 有限個であればどんなに多くても和は必ず存在し、足す順番も自由である。 そして、その和が実験値を再現するのはクーロンの法則の正しさから当然なのだ5。
ここで得られる教訓は、安易なモデル化は時に危険だ、と言う事だろう。物理屋は非常に大きな数や値はすぐに無限大として扱う。 これで大抵の場合に問題はないのだが、ここで見た結晶のマーデルング定数の様に、問題になる場合もある。その場合は慎重なモデル化が必要だ。 マーデルング定数は結晶から1つのイオンを取り出すのに必要なエネルギーを意味している。 結晶がいきなり無限に大きいと結晶の外が存在しないから、そもそも取り出すと言う操作が定義できない。 だから、結晶の外がある状況を保ちながら十分に大きくする、すなわち、結晶を常に有限サイズに保って十分に大きくする必要がある。 これだけではまだ足りない。重要なのは十分に大きくするやり方(“無限大”への持って行き方)である。 上で見た様に、立方体を大きくしていくモデルは成功するが、球体を大きくしていくモデルは失敗する。違いは何か? 立方体では常に端まで結晶の構造を尊重しているのに対して、球体では端(表面)で結晶の構造を完全に無視している。 これが致命的で球体モデルは、バルクな内部では尊重しているにも関わらず、正しい答えを与えないのだ。 少し意外だが、結晶では構造すなわちイオンの並び方が本質的に重要な事を考えれば納得できるだろう。 だから正しいモデル化は、結晶構造を端(表面)まで尊重した有限サイズで先に和をとってからサイズを十分に大きくする、 になる6, 7, 8。
物理屋は普段、全空間積分をするときに無限遠に飛ばす表面の形など気にしない。たとえ部分積分で表面項が出て来てもゼロと無視する。 しかし、それが許されるのも被積分関数次第だ、と言う基本をこのケースで再認識した。慣れって怖い。
1 大きな範囲で均して見ると分布は一様なので、この近似は悪い近似ではない。
2 「もしも宇宙が無限に広かったら夜はないはず」と言われるのも同じ理由である(本当は光が無限に速いか宇宙が無限の昔から存在していたらも必要)。 だから、地球に夜がある事実は、宇宙が無限に広くないか、あるいは無限の昔から存在しないか、の証拠である。実際はこの両方である事が判っている。
3 この状況を物理学では「べき発散(power divergence)」していると言う。クーロン力は長距離力なので無限系で常にこの種の発散が起こる。
4 物理的には不要だが、級数の新たな項を求めると言う目的で、注目するイオンの位置を固定する必要がある。 イオンの数は両側にほぼ均等に増やせば良いので、辺の長さは奇数でも構わない。つまり1辺のイオンの数は偶数でも構わない。 辺の長さが奇数だと、注目するイオンの位置は立方体の中心から少し外れるが問題ない。 むしろ、辺の長さを奇数に限った方が、立方体が電荷中性になるお陰で、部分和の数列の収束が圧倒的に速い事が知られている。 下に Python で書いたコードを置いておく。整数 N を変えて走らせて見ると良い。 N=4 すなわち1辺の長さが9の立方体で 1.74750 となる。もう既に5桁も極限と合っている。
5 より現実的には、イオン間にはクーロン力の他にここでは考慮してない短距離斥力もはたらいている。実験との比較は少し複雑になる(ボルン・マイヤーの式)。
6 有限サイズで先に和を取らないと端(表面)を指定した事にならない。
7 立方体に限らず直方体でも一部が凸になったり凹んだりした形(ブロックで作った様な)でも、結晶の構造を端まで尊重している限り、大きくしたときの極限値は同じになって、正しい結果を出すはずだ。 暇ができたらプログラムを組んで確認したい。と思ったが、立方体からの差の寄与がゼロに行く事を示せばわざわざ作る意味はないか。 この点から言うと、球体と最も近い凸形体との差の寄与はゼロに行かないから球体モデルはダメ、とも言えるだろう。
8 この部分和の数列は極限がとれる(収束する)。極限で和は無限級数になり、その中の順番を適当に変えると任意の値に収束あるいは不定にできるので、条件収束な無限級数だと言えるが、 そもそも、先に項数を無限への極限をとってから後で足し算するのは正しいモデル化に反している。
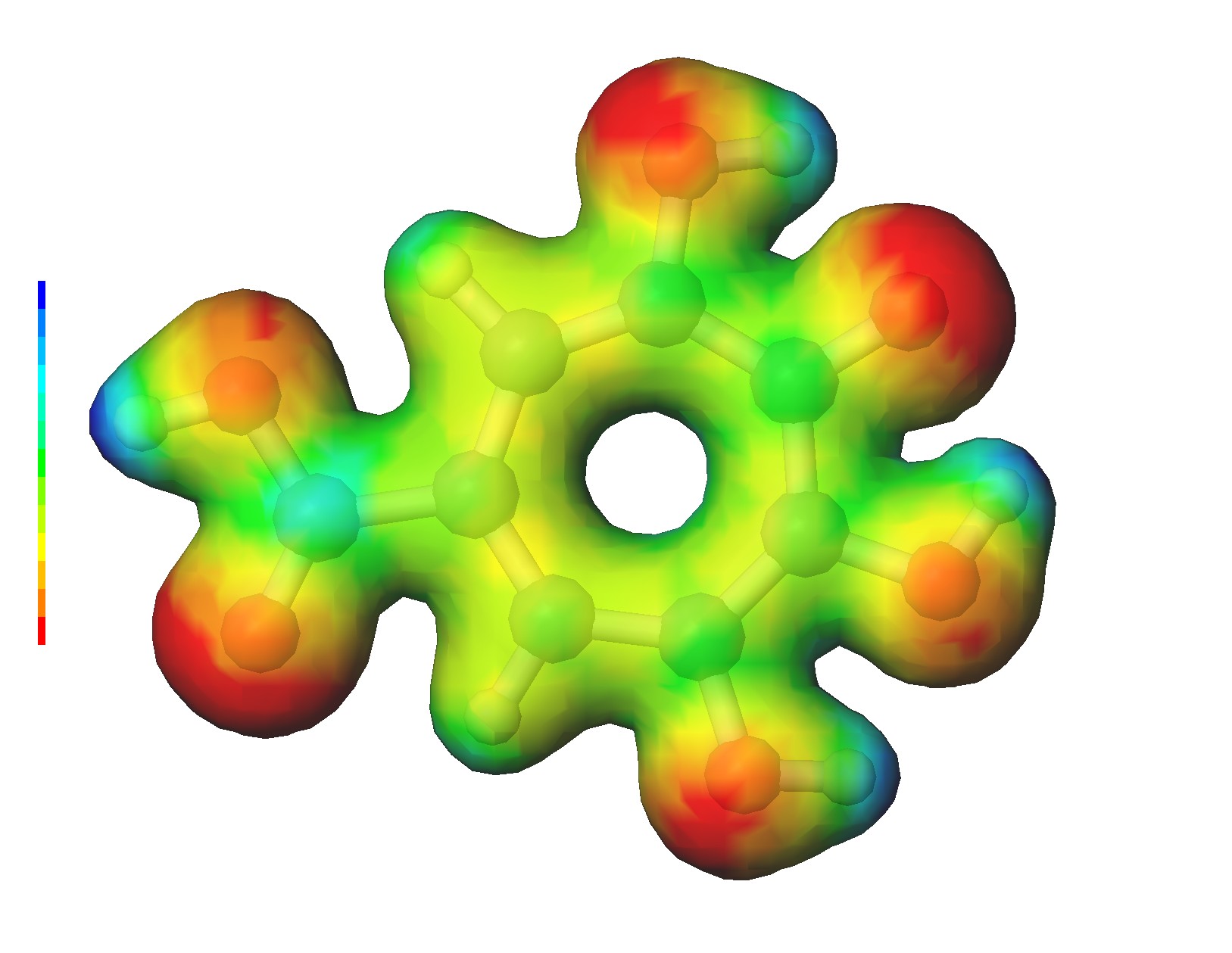
プベルル酸の電子状態
今話題のプベルル酸(Puberulic Acid)の電子状態を解いてみた。理論には B3LYP 密度汎関数理論を基底系には 6-31+G* を用いた。 平面構造なのは初期構造を平面にしたからで、もしかすると準安定構造(最安定構造ではない)かも知れない。 カルボキシル基の反対側にある水素の付く位置にもバリエーションがある様だ。炭素の七員環になっている。私にとっては新鮮だ。 非ベンゼン系の芳香族に分類されるとのこと。この分子のどこにそんな強い毒性があるのだろうか? プベルル酸の生体内での作用はまだよく分かってないらしい。こんな小さい分子でも分からない事があるとは意外だ。
プベルル酸の電子状態を解いてみて気づくのは、電子親和力(Electron Affinity)があること。 ΔSCF 法で求めた電子親和力(断熱)は以下。
