GALLERY
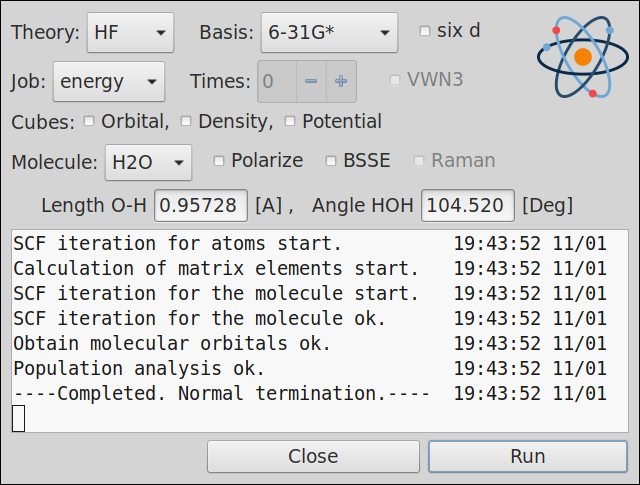
量子化学計算ソフト Titanium
趣味で作った量子化学計算ソフトです。遅いし機能も多くないのでプロの本格的なユースには向きません。 と言っても、近頃のパソコンなら小さな分子の計算はすぐに完了するので、 学生が入門として量子化学を体験して見るには良いと思います。あとは背伸びして周りを驚かせたい高校生にも。 エネルギー計算、構造最適化、振動解析、各種スペクトルの出力、軌道や密度や静電ポテンシャルの出力など、基本的な事は大体できます。 原理的には(時間を無視すれば)、任意の分子を計算できます。 量子化学計算とはどの様なものか、手元で実際に動かして学ぶ事ができます。インストールは圧縮ファイルを展開するだけです。 もしも不具合を見つけたら教えてください。 zip ファイル名を見ると分かりますが、ときどき微妙に改良してます。
Quantum chemistry calculation software, Titanium
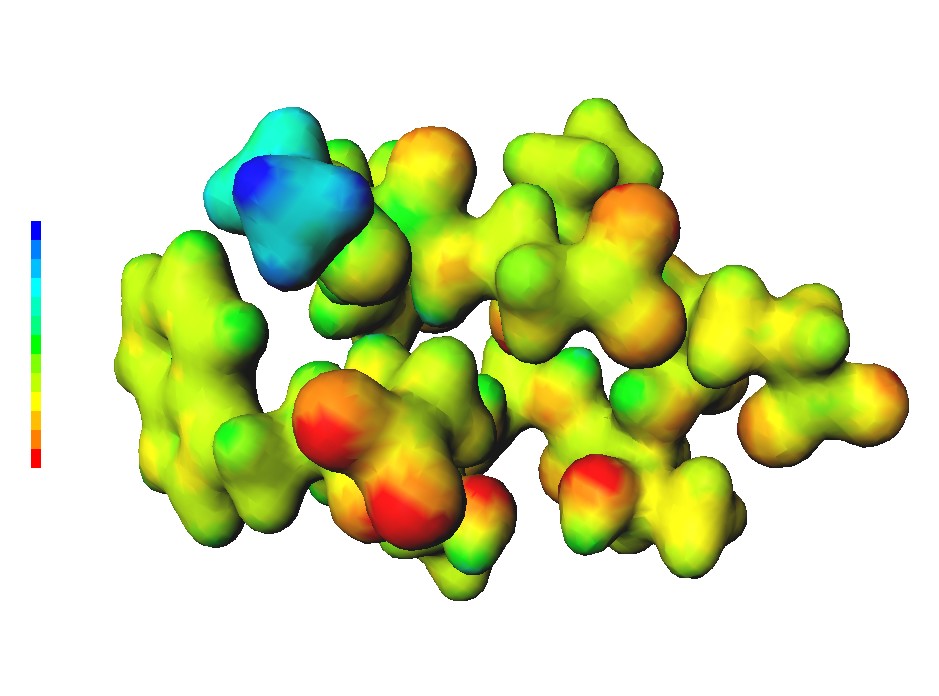
タンパク質の全電子計算
最小のタンパク質 Chignolin の全電子計算を Hartree-Fock 理論, STO-3G 基底系で行った。 原子数は 138。電子数は 570。基底数は 446。このサイズが私が自由に使える計算機と自作プログラム(↑)での限界。 アミノ酸残基が 10 個の Chignolin をタンパク質として認めるかどうかは議論の分かれる所だと思うが、 ともかくこれで、私の最初の目標であったタンパク質の全電子計算は、一応、達成できた事にしよう。
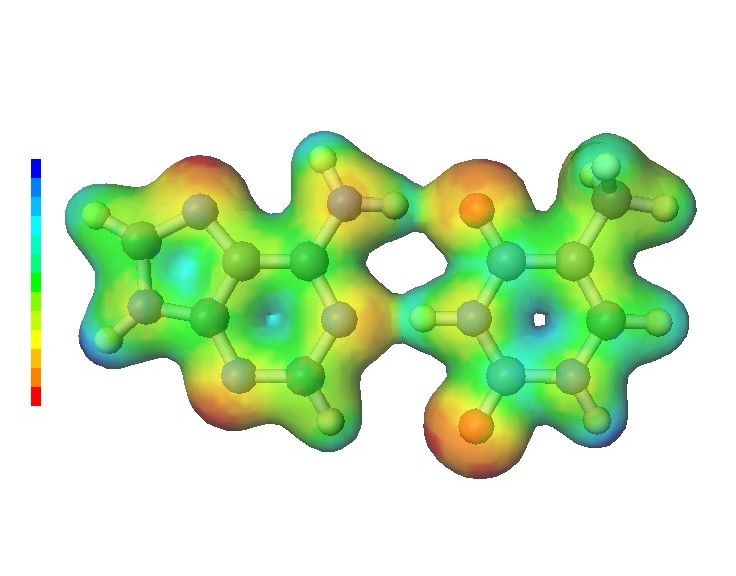
核酸塩基対の量子化学計算
前から一度見たいと思っていた核酸塩基対の水素結合を量子化学計算で見てみた。 リボース部分を水素で置き換えた、塩基部分のみを適当に離して横に並べ、 B3LYP 密度汎関数理論、6-31+G 基底系で1点エネルギー計算を行った。 電子密度をオーバラップさせると単体の合計よりエネルギーが上がることから、共有結合はしない事が分かる。 もう少し離れた距離での水素結合。(もしも共有結合だったら解離しにくくなって複製が進まないだろう。) 静電ポテンシャルマップを見ると、Adenine-Thymine で2本、Guanine-Cytosine で3本、 見事に水素結合するのが分かる。これが生命の設計図の根幹かと思うと神秘的だ。

塩化ナトリウムの分子動力学計算
Na+ と Cl− の1対1混合系の分子動力学計算をしてみた。 温度を能勢・ポアンカレ法で、圧力をアンダーセン法で制御した NPT アンサンブル。 周期境界条件な基本セルに Na+ 250 個と Cl− 250 個。 イオン間には Coulomb 力と Born-Meyer-Huggins 型の短距離力。 条件収束級数な Coulomb ポテンシャルの寄与は Ewald 法で評価。 2 [fs]の時間ステップで 250000 回の時間発展(500 [ps])を測定。 得られた動径分布関数(対相関関数)をみると、温度 300 [K] で NaCl 型の結晶に、 1200 [K] で液体になっているのが分かる。妥当な結果だ。
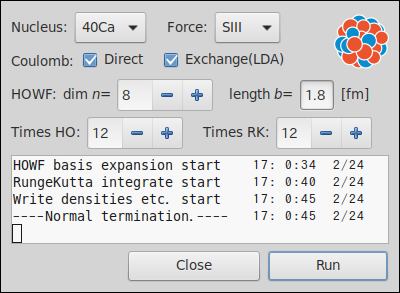
原子核密度汎関数理論計算ソフト
丸い原子核に対する密度汎関数理論(Density Functional Theory)の計算ソフト。 昔は Skyrme Hartree-Fock とか Density Dependent Hartree-Fock と呼ばれていた理論。 化学で密度汎関数理論が流行ってから、密度汎関数理論と呼ばれる事が多くなった。 原子核の分野では化学よりずっと前から密度汎関数理論のアイデアは利用されてます。問題がより難しいからです。 丸と扱ってはダメな原子核も含まれているかも。使う人は居ないと思いますが、もしも使う場合は自己責任で。 インストール方法は上にある Titanium と同じです。
64bit Windows 用バイナリ, Intel mac 用バイナリ, Apple Silicon mac 用バイナリ
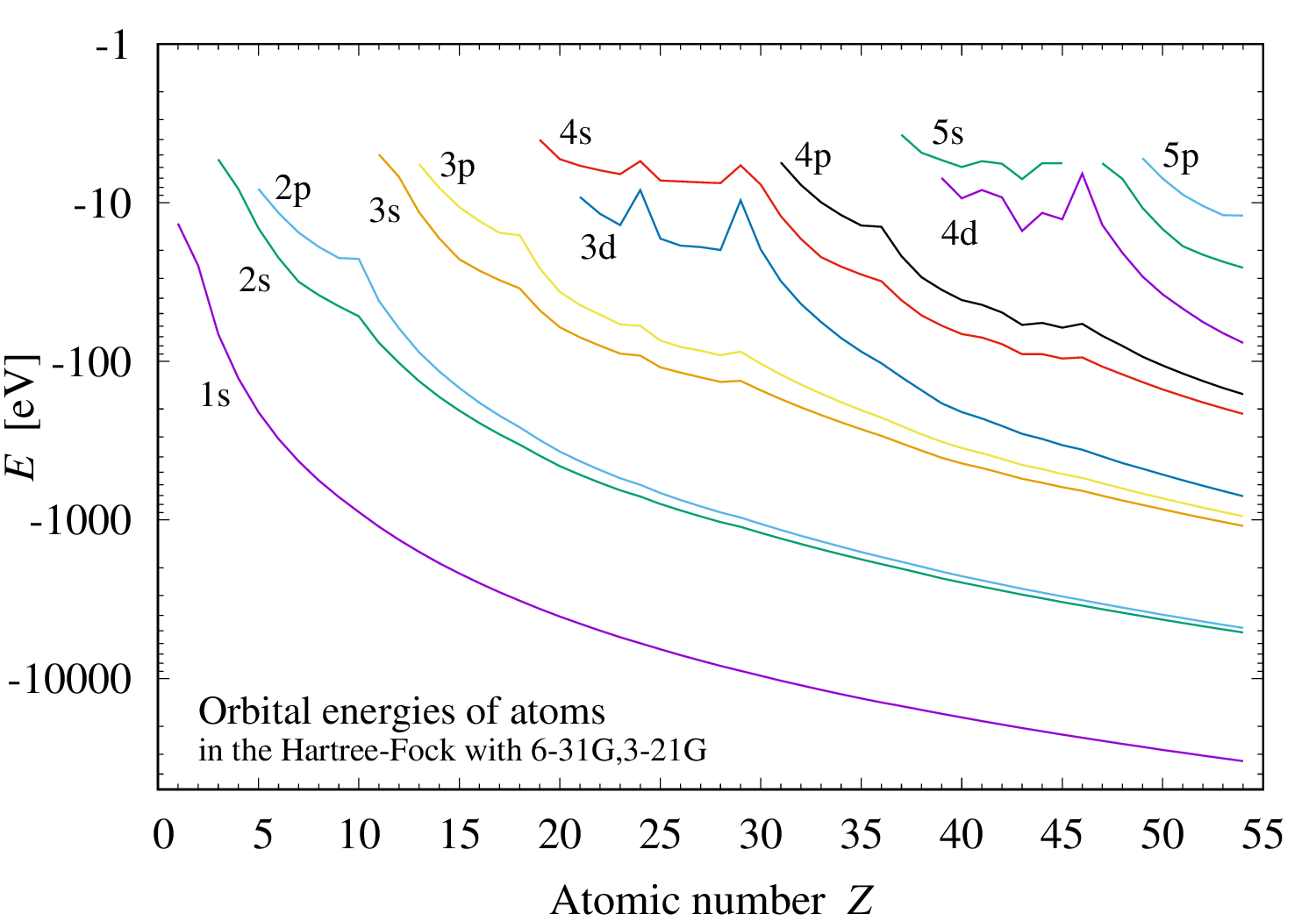
原子の Hartree-Fock 軌道エネルギー
原子の正準 Hartree-Fock 軌道のエネルギーをプロットしてみた。水素からキセノンまで。 縮約 Gauss 型基底系(Kr まで 6-31G、Rb から 3-21G)を使ったので絶対値に高い精度はないけれど、占有軌道のプロットには十分なはず。 多電子系において一粒子軌道はあくまでも道具に過ぎないが、その固有“エネルギー”は、Koopmans' 定理(近似)の範囲で、 イオン化エネルギーと対応する。プロットすると綺麗な殻構造が見て取れる。これが周期表の起源。 遷移元素の基底状態で 3d(4d) より先に 4s(5s) が埋まるのは、電子系の全エネルギーが軌道エネルギーの単純な和ではない事を示す例。 つまり、3d(4d) を空けても 4s(5s) を埋めた方が全エネルギーは低くなる。 1s 軌道のエネルギーは原子番号 30 くらいから -10 [keV] を越えている。 電子の質量は 500 [KeV] だから、精密な計算には相対論的運動学が必要だろう。 この非相対論的 Hartree-Fock 計算の結果を使って銅 Cu (原子番号29)の特性X線の波長を見積もると、 2p から 1s への遷移で 1.5545 [Å] であり、3p から 1s への遷移で 1.4004 [Å] である。 これは実測値である Kα 線の 1.5418 [Å] と Kβ 線の 1.3847 [Å] にだいたい一致している。素晴らしい。 しかし、だからと言って、正準軌道やそれに付随するエネルギーが実在する、と言う意味ではない事に注意。 これらは、あくまでも、イオン化エネルギーや特性X線の波長を見積もるときに計算が易しくなる便利な道具に過ぎない。 固有エネルギーを持たない非正準軌道の行列式で原子の全電子波動関数を表現しても、計算は難しくなるが、 イオン化エネルギーや特性X線の波長を求める事は出来る。誤解しない様に。
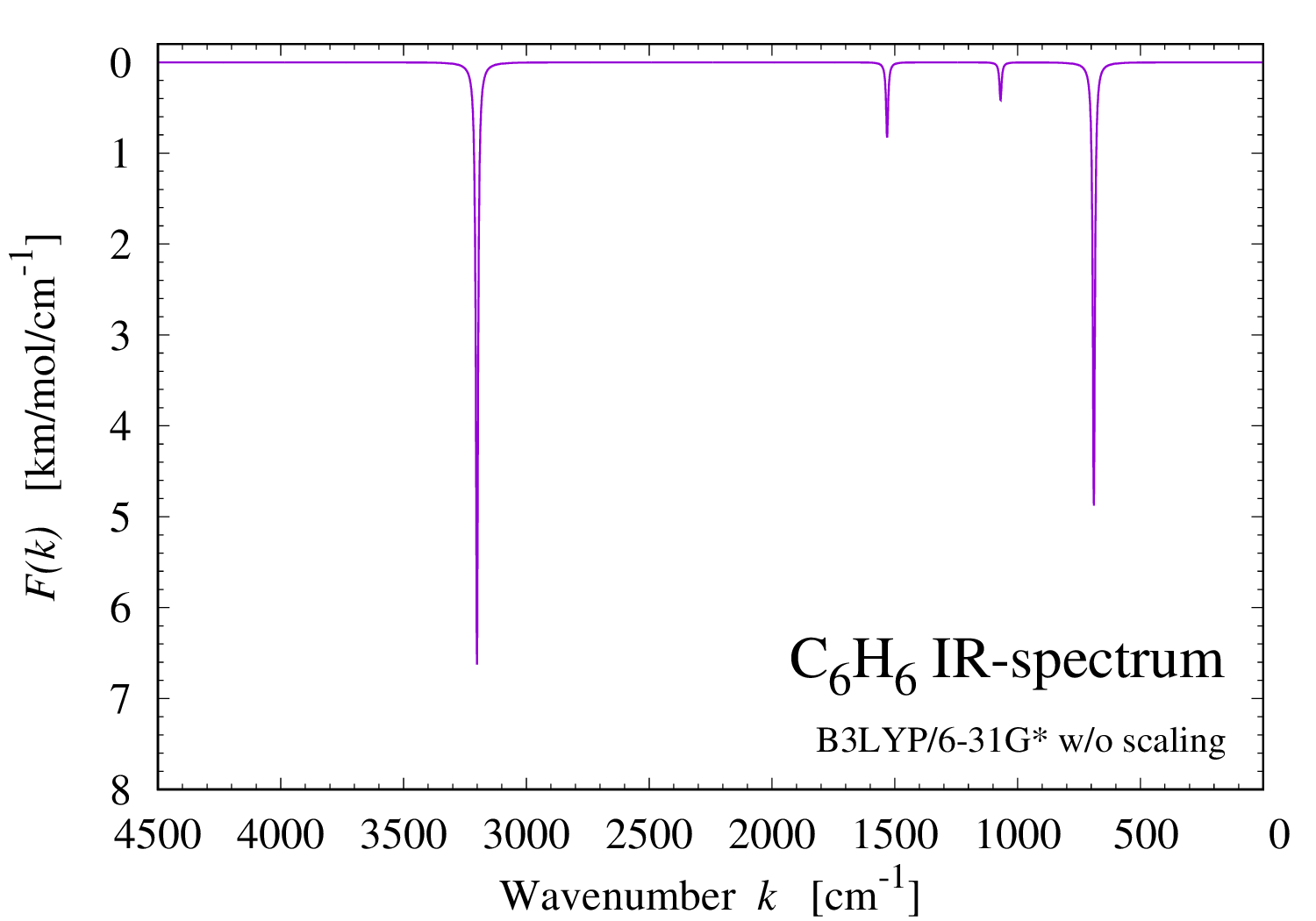
分子の赤外線吸収スペクトル
二酸化炭素など小さな分子の赤外線吸収スペクトル(IRスペクトル)を計算してみた。サムネイルはベンゼンの計算結果。 理論には B3LYP 密度汎関数理論(VWN3を含む)を、基底系には 6-31G* (D型は6種類)を用いた。 二酸化炭素の結果を見ると、確かに、CO2 分子が波数 2400 [cm-1] 辺りの赤外線を強く吸収する事がわかる。 これが、CO2 が温室効果で地球温暖化を引き起こしていると言われる所以。 非調和性の補正(スケール因子を掛ける)をしないと波数は若干大きめだが、 それでも数パーセントの範囲で実験値に一致しているのは見事だ。 ちなみに、HeH+ は宇宙で最初にできたと考えられている分子。 こちらは、永久双極子モーメント持っており、 波数 3000 [cm-1] 辺りの赤外線を非常に強く吸収する。 きっと、この非常に強い吸収はこの宇宙の構造形成に大きな影響を与えたのだろう。
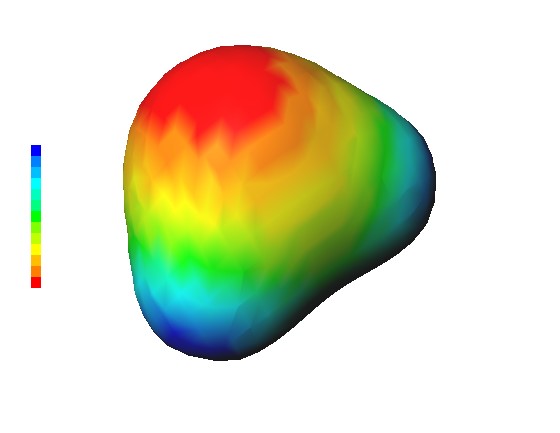
静電ポテンシャルマップの誤解
サムネイルは Hartree-Fock 近似で解いた水分子の静電ポテンシャルマップである。 静電ポテンシャルマップは、等電子密度面に静電ポテンシャル(電位)を色で表現したものであり、 新しめの化学の教科書で良く見かける。分子の特徴を捉えるのに便利だし綺麗だし、私もすぐに好きになった。 ただし、困った事に、この静電ポテンシャルマップを「表面電荷」などと説明している WEB ページや講演資料などが散見される。 化学界のジャーゴンなのかも知れないが、物理屋からすると許し難い。(もしも Poisson が聞いたら泣く。) 直接に「表面電荷」を使ってなくても同等の間違った説明はとても多い。 例えば次のような説明をしばしば見かけるが、これらは2つとも間違っている。
- 面上の赤い点は負の電荷密度を持ち、青い点は正の電荷密度を持つ。(間違いなので注意!)
- 面上の赤い点は電子密度が大きく、青い点は電子密度が小さい。(間違いなので注意!)
赤い点の電荷密度が負であるのは正しいが青の点の電荷密度も負である。もっと言うと同じ値である。 また、赤い点や青い点に限らず、面上のすべての点で電子密度は同じである。この表面が等電子密度面なのだから当然だ。 原子核の位置を除けば空間には電子しかないのだから、面上の電子密度と電荷密度は電子の電荷倍を除いて同じである。 よって、電荷密度もこの表面上のすべての点で同じ値である。
この図の正しい説明は、等電子密度面が、酸素の周りで原子核から遠くにあり面上の電位が負に、 水素の周りで原子核の近くにあり面上の電位が正になっている、である。 ここで、電位と言うのは単位電荷の獲得する位置エネルギーであり、静電ポテンシャルとも呼ばれる。 だから、この図が意味しているのは、プラスの電荷たとえば陽子をこの分子に近づけたとき、 青の場所に来るとプラスの位置エネルギーを持ち、赤い場所に来るとマイナスの位置エネルギーを持つ、 と言う事である1。 一般に電荷に限らず全ての物体は位置エネルギーが最も下がる方向に力を受ける。 だから、例えば陽子がこの分子に近づいたとき、青い部分に近づくと反発力を受け、赤い部分に近づくと引力を受ける。
この分子で等電子密度面が原子核から遠くに/近くになるのは、その外場で 10 電子系の量子力学を解いた結果、 つまりダイナミクスに他ならないが、結果として酸素原子が電子を引きつけ水素原子が電子を与えた事による。 だから、次のような説明なら間違っていない。
- 赤い所にある原子は負の(部分)電荷を持ち、青い所にある原子は正の(部分)電荷を持つ。
- 赤の奥にある原子核の周りは電子が多く(孤立原子のときと比べて)、青の奥にある原子核の周りは電子が少ない(同左)。
正の電荷は、正の電荷の近くほどプラスの位置エネルギーを持ち反発力を受け、 負の電荷の近くほどマイナスの位置エネルギーを持ち引力を受ける。 だから、静電ポテンシャルマップの色を「表面電荷」と考えたり呼んだりしたくなる気持ちは分からないではない。 そう考えれば、上で書いた、分子に近づいた陽子が受ける力を定性的に説明できる。 また、2つの分子が接近・反応するとき、静電ポテンシャルマップで見ると、 一方の分子の赤い部分と他方の分子の青い部分が接近・反応し易い。 これも正電荷と負電荷が引き合うと考えれば接近・反応について正しい予想が得られる。 だから「表面電荷」が便利であるのは間違いない。それでも、簡易的に正しい予想を導く便利な道具に過ぎない。 この辺りをちゃんと分かっていて、道具として比喩として「表面電荷」や類似の説明を使うのであれば良いが、 どうも分かっている人ばかりではない様に見える。 特に物理学(電磁気学)を学んだ事がない人は、上の 1.,2. が文字通り本当だと何も考えずに信じている様である。残念だ。 だから化学界には、たとえ比喩だとしても、誤解を生む危険な比喩は使わないで貰いたい。 そして、学生達に電磁気学の基本的な部分だけでも学ばせて欲しい。
1 マイナスの電荷たとえば電子を近づけると逆になる。 すなわち、青の場所でマイナスの位置エネルギーを持ち、赤の場所でプラスの位置エネルギーを持つ。
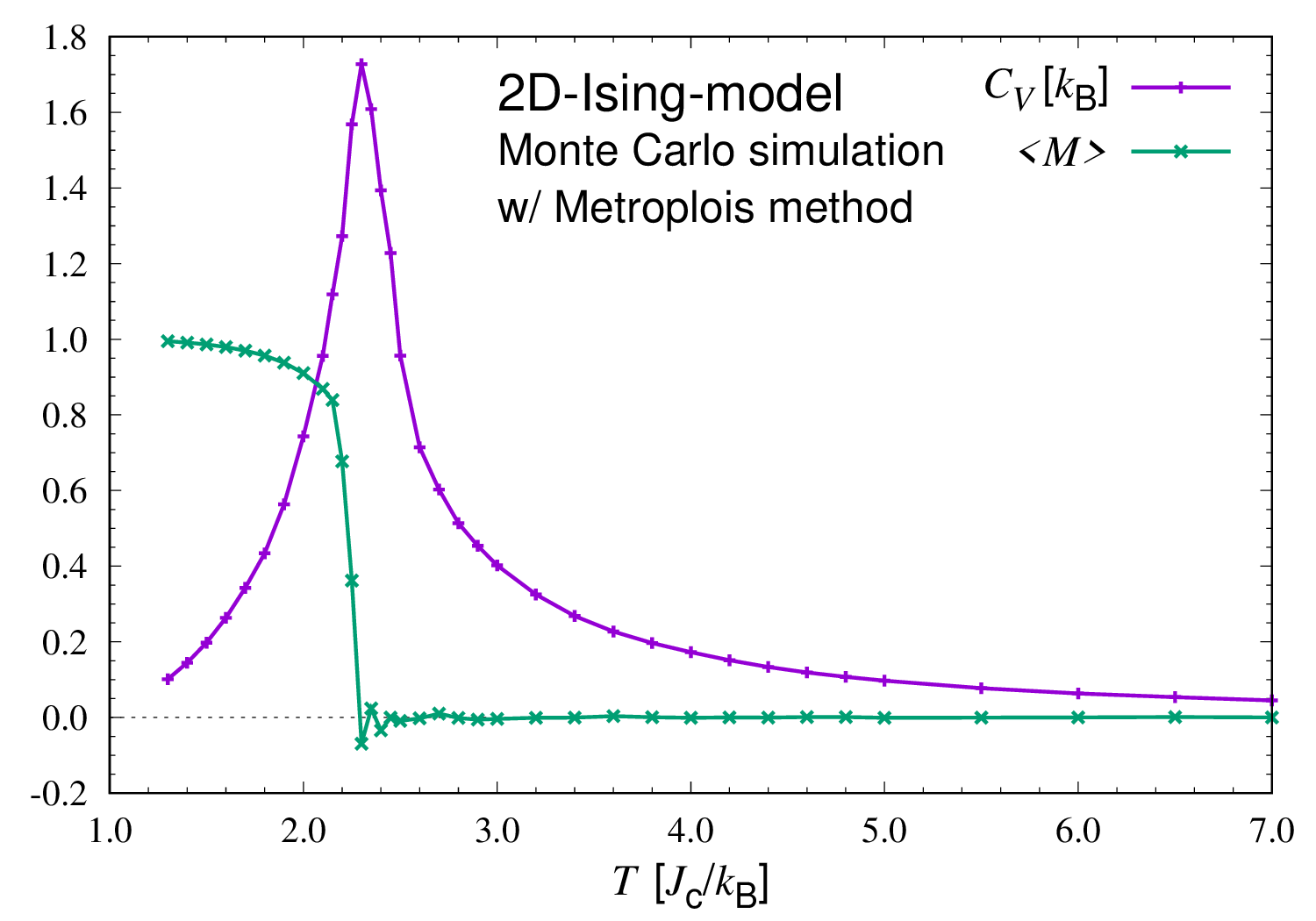
2次元 Ising 模型のモンテカルロ計算
2次元の Ising 模型をモンテカルロ計算した結果。かなり前にやったものだが載せておく。 Ising 模型は磁性体の一番簡単な模型。スピンの数は縦横 20 × 20 の 400 個とした。 Monte Carlo(モンテカルロ)計算は乱数を使った統計力学の計算手法。サンプリングには Metropolis(メトロポリス)法を採用した。 Heat-bath(熱浴)法もやってみたがこの例では効率に大きな差はなかった。 温度を変えて計算。各温度で 4000000 回(10 kmcs)の Thermalization (熱平衡化)の後、24000000 回(60 kmcs)の測定。 結果を見て分かるのは、温度を上げて行くとある温度で磁化が消滅すること。そして、その温度で比熱の発散(の片鱗)も見える。 磁性体の相転移現象をよく再現できている。
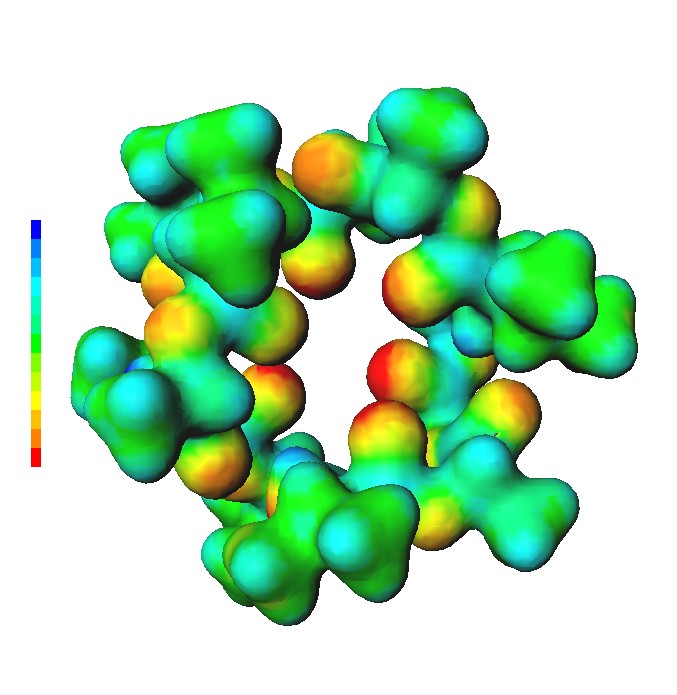
バリノマイシンの全電子計算
Valinomycin の全電子計算を Hartree-Fock 理論, 3-21G 基底系でやってみた。 原子数は 168。電子数は 600。3-21G 基底系での総基底数は 882 で、2電子積分のサイズは 126 [GB] になる。 普通の計算機では無理だが、同僚がメモリーを載せまくった Xeon 計算機を購入したので、借りてやってみた。 Valinomycin はアミノ酸が12個つながって輪になった分子で、環状ペプチドに分類される。 輪の中にカリウム陽イオンを収めて、そのままでは通過できない細胞膜を通過させる働きをするらしい。 この様な分子をイオノフォアと呼ぶそうだ。 一部の菌がこの分子を作って他の菌を殺すのに使っているとの事。いわゆる抗生物質。 攻撃された菌は細胞の中がカリウム陽イオン過剰になり、必要な反応が進まなくなって死ぬのだろう。 なぜ製造元の菌が死なないのか、生物学素人の私には分からないが、何か仕組みがあるに違いない。 この分子の等電子密度面を表示したとき、その見事な形に感動した。 綺麗なドーナツ形状をしている(ミスドのフレンチクルーラーみたいだ)。 中の空洞の広さがカリウム陽イオンの大きさとぴったりらしい。 しかも、空洞の内壁には酸素原子が配置されていて陽イオンを取り囲んで安定的に保持する。 さらに、リングのパーツは可動式で口が開いたり閉じたりできるらしい。何と良くできた分子だろう。 この様な例は、生命も原子のみでできていると言う事実を再認識させてくれる。 この分子の形は Interactive 3D view で回したり拡大したりすると良くわかります。堪能してください。
