GALLERY 2
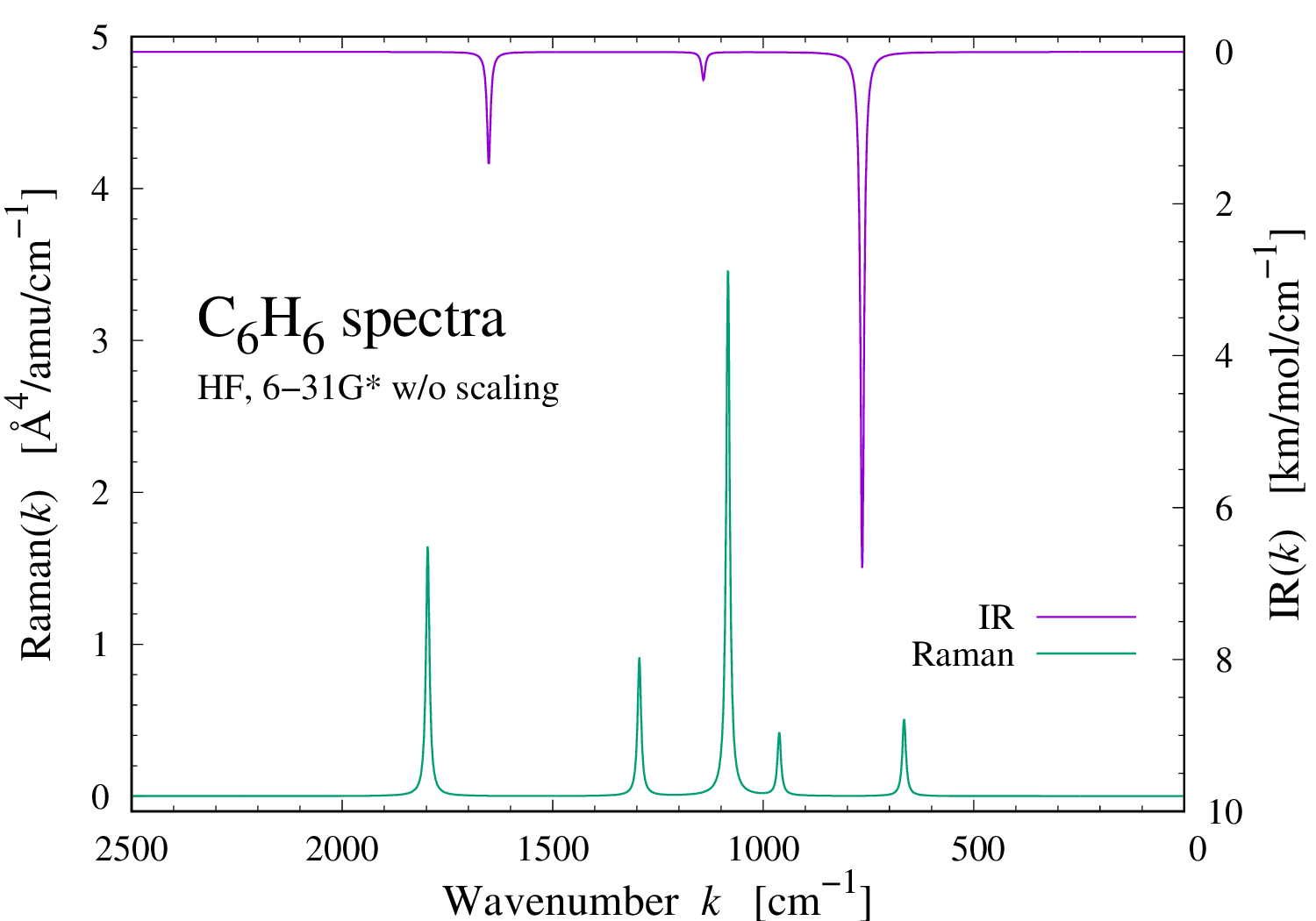
ベンゼンのラマン散乱スペクトル
Benzene C6H6 の振動ラマン散乱スペクトルを計算してみた。 ラマン散乱強度の計算は時間がかかるので Hartree-Fock 理論を使った。基底系は 6-31G* を使った。 得られた強度を適当の幅(10 [cm-1])の Lorentzian で畳み込んでスペクトルにしている。 結果を見ると、赤外線吸収と Raman 散乱が見事に排他的になっているのが判る。 これは Benzene が対称中心を持つことから従う選択則。 一番低い基準振動(453 [cm-1])や下から4番目の基準振動(777 [cm-1])などは、 赤外線吸収も Raman 散乱も不活性である。つまり、振動による分子の変形の1次で、双極子モーメントも分極率も変化しない。 双極子モーメントの方は容易に想像できるが分極率の方は難しい。 原子核が動けば、電子分布が動いて分極率も変わって当然の様に思える。 原子核が協調して動いて電子分布が変化しないのだろうか? それとも、電子分布が変化しても特殊な変化で1次の範囲では電場への応答性が変化しないのだろうか? いずれにしても、面白い振動があったものだ。 Benzene を含む幾つかの分子の基準振動は岡山理科大学の こちらのページ で見る事ができます。
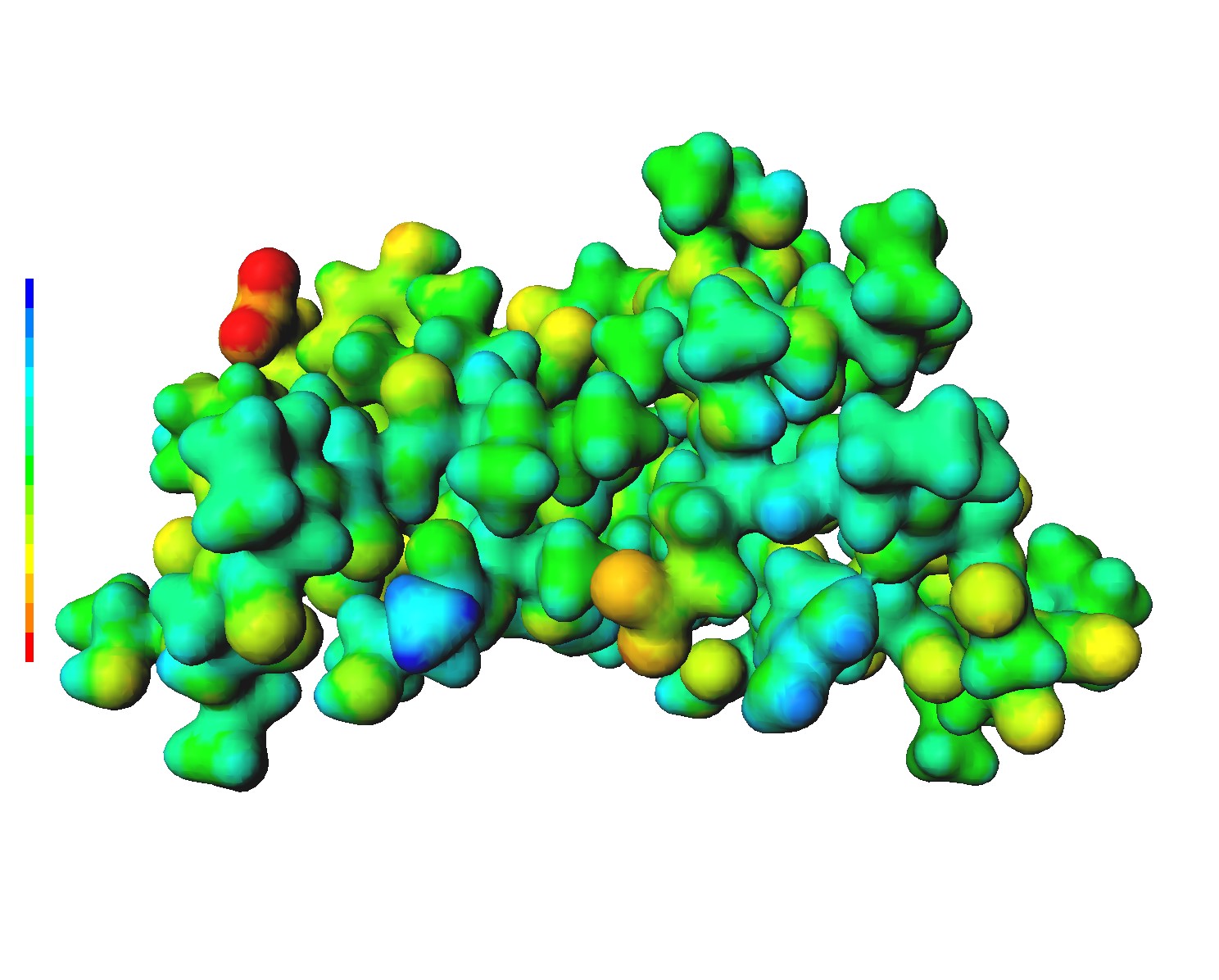
クランビンの全電子計算
タンパク質 Crambin の全電子計算を Hartree-Fock 理論, STO-3G 基底系でやってみた。 原子数は 642 で、電子数は 2520。STO-3G 基底系での総基底数は 1974 で、2電子積分のサイズは 825 [GB] にもなる。 普通のパソコンはもちろん、メモリーを載せまくった同僚の計算機でも無理だが、 メモリーを超載せまくった Xeon 計算機にアカウントを貰ったので、空いてる時間を見計らってやってみた。 Crambin はアミノ酸残基が 46 個のタンパク質で、キャベツの種子にある本物のタンパク質。 これまでは最小タンパク質(自称)の Chignolin で納得していたが、今回めでたく本物のタンパク質の全電子計算に辿り着く事ができた。 と言っても、巨大なメモリーの恩恵にあずかっただけだが。また、Crambin はタンパク質の中では最も小さい部類。 アミノ酸残基数が 300 を越えるインスリン六量体などを相手にしている専門家達には遠く及ばない。 私のプログラムでも2電子積分を使い捨てにする Direct SCF を使って原理的には対応可能だが、 時間が掛かりすぎて現実的には無理だろう(試す気も起きない。最も小さな Crambin でさえも)。 データが大きいせいか、静電ポテンシャルマップでは JSmol でエラーが発生するので、Interactive 3D view は骨格のみ。 骨格だと分子の中が良く見える。Crambin の中を見るとジスルフィド結合と思しき S-S 結合が3箇所あるのが判る。 きっと、これらの結合がこのタンパク質の folding と構造安定化に決定的な役割を果たしているのだろう。 JSmol がエラーになるページへのリンクも張っておきます。原因や対処法が分かる人がいましたら連絡ください。
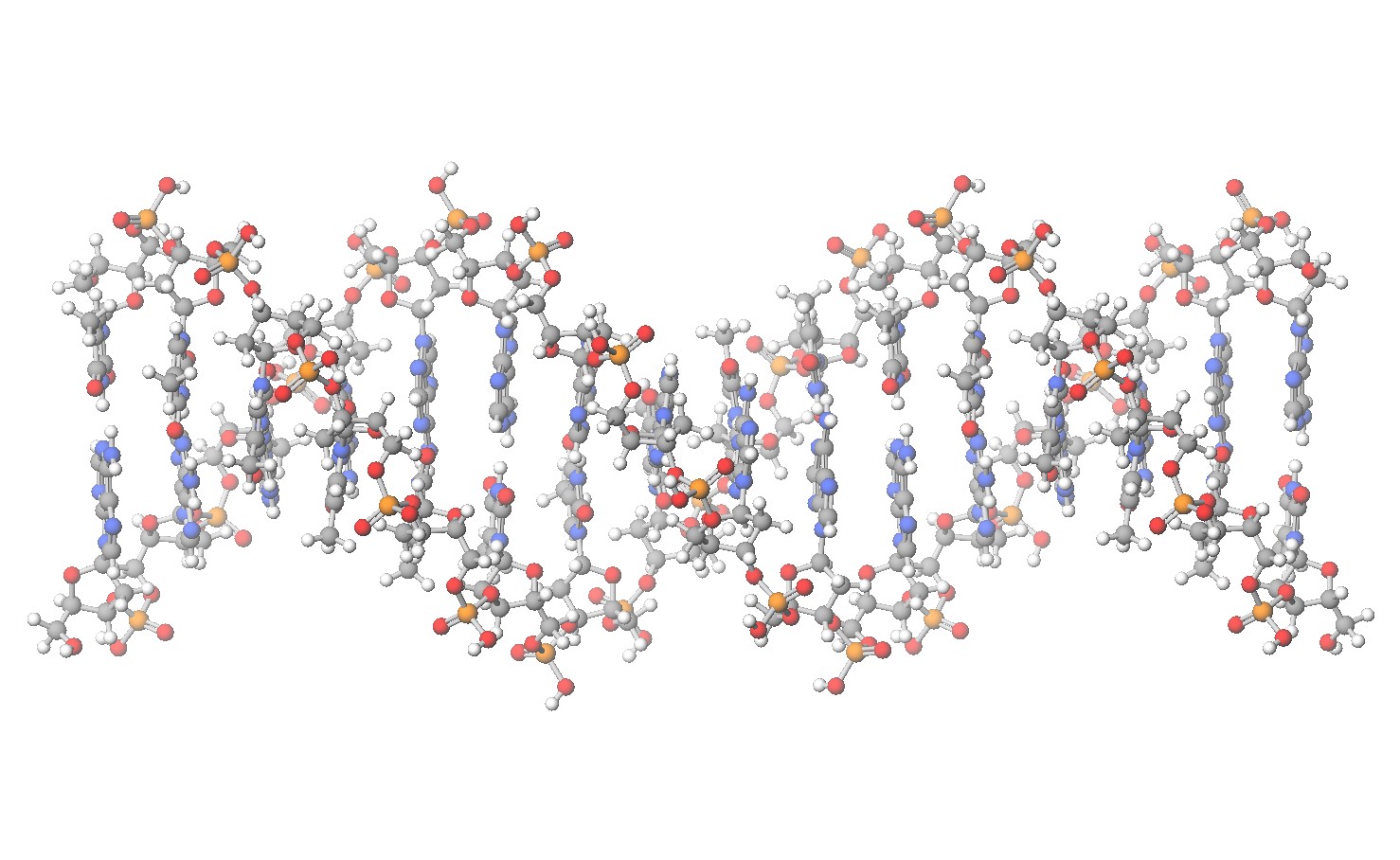
DNA の二重らせん
論文の付録にデオキシリボ核酸(DNA)の原子配置があったので JSmol で表示してみた。 ヌクレオチド16対(32個)分。塩基配列は不明。これくらいあると二重らせん構造が見て取れる。 また、回しながら見ると、狭い隙間と広い隙間が交互にあるのも分かる。 この様なごく一部でも、原子数は 1052 で、総電子数は 5060 になる。 STO-3G 基底系を使っても2電子積分のサイズが 2 [TB] を越えるので電子状態計算は諦める。 軸方向から眺めると、窒素が内側に酸素が外側に偏っている。 これは一般的なのか?それともこの塩基配列が特殊なのか?知っている人がいたら教えてください。 中の水素結合が見やすい様に、ヌクレオチド4対分と1対分も載せておきます。
水分子の基準振動モード
JSmol で分子の振動モードを表示する方法が分かったので、備忘録として水分子の例を下に載せておく。 こうやって見ると、3種類の基準振動モードの違いが良く解る。 Mode 1 から順にそれぞれ、変角振動、対称伸縮振動、非対称伸縮振動と呼ばれる。 誤解しないで欲しいのは、これらの表示はあくまでも基準振動の変位ベクトルを示すものであって、振動数はまったく正しくない。 実際の振動数は 100 [THz] (テラヘルツ,1012 Hz) ほどなので、ずっとずっと速い。目で追えない速さ。 ちょうど赤外線の振動数に対応しているので、分子は振動で赤外線を吸収したり放射したりする。 それから、実際は振幅もこんなには大きくないであろう。つまり、これらの表示はモードの違いを分かり易く見るためだけのものである。
フッ化リチウムの結晶
結晶構造も回して見ると分かり易いのでフッ化リチウムの例を載せておく。 リチウムとフッ素がともに面心立方格子になっている。原子を区別しないと単純立方格子になっている。いわゆる NaCl 型の結晶。 ついでに、体心立方格子(BCC)と面心立方格子(FCC)と六方最密充填格子(HCP)の単位胞も載せておく。
結晶中の電子状態を求めるには、周期境界条件を設定して無限系にする必要がある。 そして、平面波基底系を使って運動量空間(逆空間)で無限電子系の Schrödinger 方程式を解く (局在基底系を使う方法もある。Tight-binding method)。 この様な計算は個体物理においてバンド計算と呼ばれる。電子のエネルギー準位が密になってバンド(帯)の様になるからである。 平面波で局所的な構造を表すのは難しいので、しばしば、内殻電子を原子核に組み込んで擬ポテンシャルにし、価電子だけを解く近似が使われる。 私はこの近似が残念で計算プログラムはまだ作っていないのだが、いずれ暇が出来たら作ってみようと思っている。
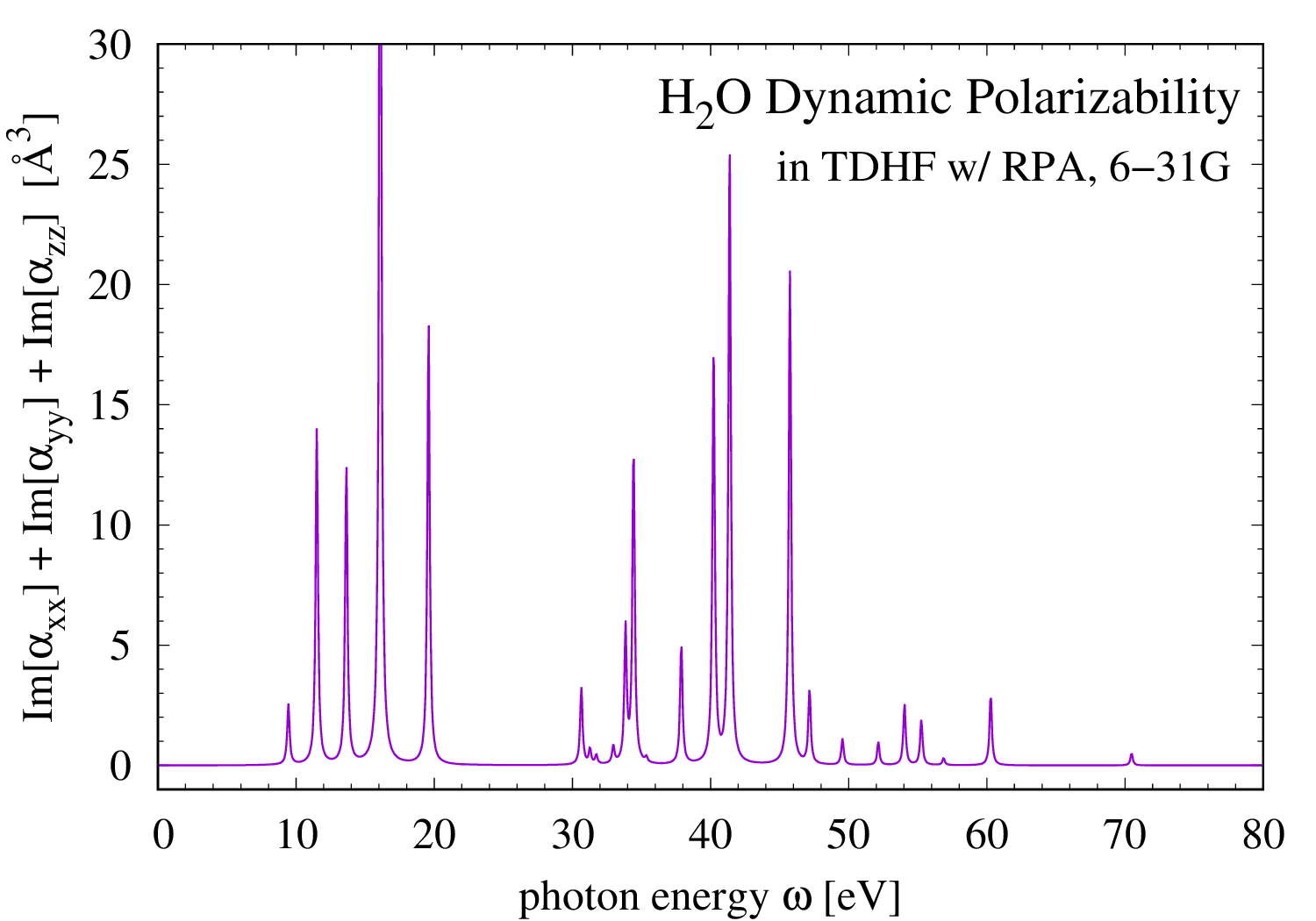
水分子の動的分極率
水分子(H2O)の動的分極率を時間依存 Hartree-Fock 理論(TDHF)と乱雑位相近似(RPA)を使って計算してみた。 動的分極率は、振動する電場を加えた時の分極率であり、電磁波に対する分子の応答を表す。 電磁波の量子である光子のエネルギーが分子の励起エネルギーに一致したとき、分子はその光子を吸収し、動的分極率は発散する。 数値計算では、発散を避けるために光子エネルギーに小さな虚部を導入し、動的分極率も複素数にする。 サムネイルは 6-31G 基底系を使って計算した H2O の動的分極率テンソルの虚部の和を、 光子エネルギーを横軸にプロットしたものである。分極率の発散すなわち光の吸収に対応するたくさんのピークが見える。 6-31G 基底系を使った RPA 計算に依れば、これらのエネルギーの所に水分子の励起状態があると言うことである (正確に言うと、振動電場で遷移できない励起状態はこのグラフに寄与しないので、振動電場で遷移可能な励起状態が、である)。 だたし、高エネルギーな励起状態の数やエネルギーは、計算に使ったヒルベルト空間の広さに強く依存するので、6-31G 基底系を使ったこの結果にあまり意味は無い。 低いエネルギーに注目すると、9.5 [eV], 11.5 [eV], 13.7 [eV] の所に吸収のピークがある。 これらはどれも紫外線の領域である。可視光領域 1.6 [eV] から 3.1 [eV] には吸収のピークは1つもない。 つまり、水分子が可視光をまったく吸収しない事を示している。これは、水が無色透明であると言う我々が良く知る事実を、量子化学から説明している。 もっと大きな分子になると、吸収が可視光領域に現れ、吸収の位置に依って分子は固有の色を持つ。 精度の高い量子化学計算はそれもだいたい再現できる。例えば、メチルイエロー(Methyl-Yellow)の例が PC CHEM BASICS の こちらのページ にある。
テトロドトキシンの全電子計算
ふぐが持つ事で知られる猛毒のテトロドトキシン(Tetrodotoxin,TTX)が意外にも小さい分子だと知ったので全電子計算をやってみた。 TTX の化学式は C11H17N3O8 で原子数は39個。 これくらいなら全電子計算も手元のパソコンで余裕だ。理論は B3LYP を使い、基底系は 6-31G を使った。 こうして見ると、TTX は何の変哲もない普通の分子である。強いて特徴をあげると、立体的に小さくまとまっている事くらいか。 ところが、この形と電子分布が神経細胞の表面にあるナトリウムチャンネルのある部分にぴったりとはまるらしい。 TTX がはまると神経細胞へのナトリウムイオンの流入がブロックされ、神経伝達が止まり、神経が麻痺してしまう。 だから、生物は TTX が体内に入ると、筋肉が正常に動かなくなり、重症の場合は死亡する。恐ろしい分子があったものだ。 ふぐ自身は遺伝子の変異によってナトリウムチャンネルを構成する部品が少し変化していて、TTX に耐性があるらしい。ずるいね! この TTX は高温にとても強いとの事。300 [℃] でも変形も分解もしないそうだ。 コンパクトにまとまっていて結合が強いから、変形も分解もしにくいのだろう。 Interactive 3D view で回しながら見ると分かるが、確かに強そうな分子だ。 ちなみに、B3LYP, 6-31G 計算に依ると、TTX は自由な原子たちから 163 [eV] 束縛している。 TTX が分解する時にどこで切れるのか分からないが、きっとそこの結合エネルギーも十分に大きいのだろう。
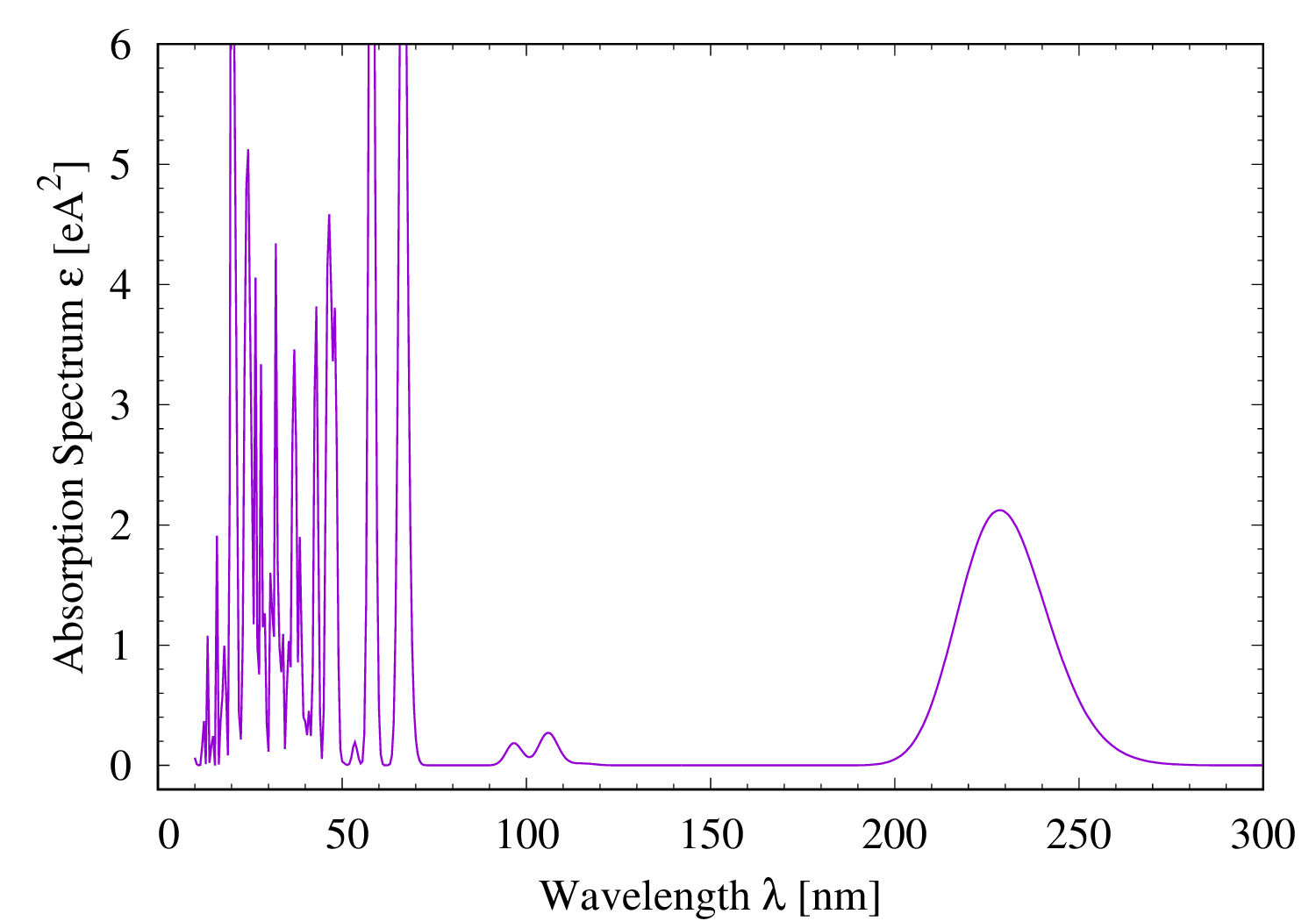
オゾンの紫外線吸収スペクトル
オゾン分子 O3 の紫外線吸収スペクトルを時間依存 Hartree-Fock 理論(TDHF)と乱雑位相近似(RPA)を使って計算してみた。 基底系には 6-31G* を用いた。 オゾン分子は、宇宙から地球に降ってくる紫外線のうち UV-C と呼ばれる波長が 100 [nm] から 280 [nm] の領域の大部分を吸収する。 分子の紫外線可視光の吸収は分子内の電子励起によって起こる。 電子励起状態に対する RPA 計算は信頼性が低い(エネルギーが高めに出る)事が知られているが、 オゾンの結果を見ると、一応、 UV-C 領域に吸収ピークが認められる。 より精度の高い時間依存密度汎関数理論(TDDFT)の計算では、波長 50 [nm] から 150 [nm] にも吸収ピークが現れるとの事1。 オゾン分子の吸収が弱い波長 150 [nm] から 200 [nm] は酸素分子 O2 が吸収するのだそうだ。 私たちの様な生物が陸上に進出できたのは、これらの分子が有害な紫外線を吸収して地上まで届かなくしてくれたお陰である。 そう思って計算結果を見ると感慨深い。もちろん、人間の活動で上空のオゾン層を破壊してはいけない。
二酸化炭素の比熱
二酸化炭素は3原子分子であるが直線分子なので、理想気体としたときの定圧モル比熱は2原子分子と同じで、 気体定数 \(\mathrm{R}\) を使って \( \left( \frac{3}{2} + 1 + 1 \right) \mathrm{R} = \frac{7}{2} \mathrm{R} \) である。 一方、標準状態(298.15 [K], 105 [Pa])での実測値は 37.11 [J/(mol.K)] であり、 これを \(\mathrm{R}\) 単位で表すと、4.4633069 [R] である。理想気体での予想から約 1 [R] も大きい。 この差はどこから来るのか?分子間力の寄与だろうか?気相だからそれはあり得ない。 正解は分子振動の寄与である。すなわち、分子内の原子核が振動運動し、分子が変形する自由度の寄与である。 例えて言うと、二酸化炭素分子は、バネと見なしたときのバネ定数が小さく、分子変形振動が励起し易いので、 常温付近でもその寄与が無視できないのである。 分子変形振動は1個の分子の性質だから量子化学の出番である。と言う訳で早速やって見よう。
二酸化炭素分子 CO2 の振動解析を B3LYP3 密度汎関数理論と 6-31G* 基底系を用いてやってみた。 非調和性の補正因子に 0.9603 を用いた。まず、得られた基準振動モードの振動数は、対応する電磁波の波数(\(k\))で表すと、 615.38 [cm-1], 615.38 [cm-1], 1316.39 [cm-1], 2336.59 [cm-1] である。 この波数から各振動モードの励起エネルギーが \(E = h c k \) と求まり、これが小さいほどその振動モードの励起が起き易い。 励起エネルギーをボルツマン定数(\(k_{\mathrm{B}}\))で割った値は便利な量であり、振動温度と呼ばれる。 それぞれ、885.40 [K], 885.40 [K], 1893.99 [K], 3361.83 [K] となる。 最初の2つは標準温度 298.15 [K] と比べて3倍弱しか違わない。この近さが常温付近で無視できない振動励起の寄与を生む。 この2つの振動モードは分子が折れ曲がる振動(変角振動)であり、下の Mode 1 と 2 で見る事ができる。 ちなみに、同じ計算で水素分子 H2 の振動温度は 6152.44 [K] であり、数千度の高温でない限り振動励起の寄与は無視できる事が判る。 分子振動の寄与も含めると、二酸化炭素の標準定圧モル比熱は 4.5779451 [R] = 38.0632 [J/(mol.K)] と求まる。 少しオーバーしたが、だいぶ実測値に近い。なかなか良い計算結果である。 それにしても、比熱の様な室温で簡単に測れる量にも量子力学の効果が確認できるとは意外で面白い。

メタンの燃焼熱
都市ガスの主成分はメタン CH4 である。だから、ほとんどの人が家で料理をする時にメタンを燃焼させている。 例えば、1 [L] の水を沸かす(温度を 20 [℃] から 100 [℃] にする)場合を考えよう。 メタンの燃焼熱は 802 [kJ/mol] (低位発熱量)なので、水の比熱を 4.2 [J/(g.K)] で一定とすると、0.42 [mol] のメタンが必要である。 数にすると 2.5 × 1023 個。体積にすると 9.4 [L]。実際には鍋や周りの空気も温めるからこれ以上に使う。 この様に料理などを可能にしてくれる、我々にとってありがたいメタンの燃焼熱であるが、一体どこから来るのだろうか? 答えは各分子が固有に持つエネルギーの差である。メタンの燃焼では次の反応が起こる。 CH4 + 2 O2 → CO2 + 2 H2O つまり、反応前の1個の CH4 と2個の O2 が、 反応後には1個の CO2 と2個の H2O になる1。 この前後で各分子が固有に持つエネルギーの合計が減少し、その減少分が燃焼熱として発生する。 分子が固有に持つエネルギーは分子の性質だから量子化学の出番である。と言う訳で早速やって見よう。
メタン分子 CH4 の燃焼熱を量子化学計算で求めてみた。まずは、Hartree-Fock 理論から。基底系は 6-31+G** を使った。 各分子のエネルギーと、反応前後それぞれでの合計と、その差は下の様に求まる2。
| CH4 | O2 | CO2 | H2O | Before | After | Diff |
|---|---|---|---|---|---|---|
| -40.15655 | -149.61563 | -187.62470 | -76.00749 | -339.38782 | -339.63967 | -0.25185 |
単位は原子単位 [a.u.] 。原点は全ての原子核と電子が無限に離れて止まった所に取っている3。 表の結果を見ると、僅かだが後の方がエネルギー合計が下がっているのが分かる(物理学で標準の原点だと割合にして僅か 1/1000 !)。 その差 0.25185 [a.u.] = 6.85 [eV] を 1 [mol] あたりの [kJ] に直すと 661 [kJ/mol] になる。 なかなか良い結果である。正しく発熱反応である事を再現しているし、発熱量の大きさも実測値 802 [kJ/mol] とだいたい合っている。 発熱にならない可能性すらあると思っていたので驚いた。 「Hartree-Fock 理論は化学が要求する精度にない」と言われるが、この例を見ると、HF 理論も捨てたものではない。 ただし、この例が特殊でそこそこ良い結果は偶然なのかも知れない。
次に、化学者お気に入りの B3LYP3 密度汎関数理論で同じ計算をしてみた。結果は下の表の通り。
| CH4 | O2 | CO2 | H2O | Before | After | Diff |
|---|---|---|---|---|---|---|
| -40.48007 | -150.32161 | -188.57658 | -76.41068 | -341.12330 | -341.39794 | -0.27465 |
分子1個で 0.27465 [a.u.] は 721 [kJ/mol] である。多少改善したが期待した程にぴったり実測値を再現とはならなかった。 使用した基底系 6-31+G** が貧弱だったか。あるいは、実測値からの外れが 10% は十分に良い結果と見るべきか。 HF 理論の結果が良かったせいでハードルが上がっているのかも知れない。 他の分子、例えばプロパン C3H8 ではどうか、試して見るのも面白い。 いずれにしても、化学反応の特性が基礎理論からパソコンを使って簡単に再現したり予測したりできるのは素晴らしい。
追記:プロパンでも計算してみた。C3H8 の燃焼熱の実測値 2043 [kJ/mol] (低位発熱量) に対し、 標準反応エンタルピーの計算結果は、HF,6-31+G** では 1711 [kJ/mol] で、B3LYP3,6-31+G** では 1860 [kJ/mol] だった。 メタンの場合と同じく、HF 理論も捨てたものではないし、B3LYP3 では改善はするがぴったりではない。HF 理論の善戦はメタンに限った偶然ではなさそうだ。 上の表を見比べて判るのは、相関欠如の影響は、各分子ではそれなり(1 [a.u.] 程度)にあるが、反応前後での合計でほぼ同じで、 反応熱ではかなり相殺されている、と言うこと。これが HF 理論の結果が大きく外れない理由だろう。 要するに、反応熱に本質的な分子固有のエネルギーの差に関しては、 独立粒子近似または平均場近似の HF 理論で大部分が取り込めている、と言うことである。素晴らしい。 もっとも、化学者はこの程度では満足しないでしょうが。 その点から言うと、現象論的パラメータをたくさん使った B3LYP3 はもっと頑張るべきだ。 もっとリッチな基底系を使えばぴったりの結果を出すのだろうか?知ってる人が居たら教えてください。
追記:メタンCH4 の燃焼熱を B3LYP3, aug-cc-pVDZ でも計算してみた。736 [kJ/mol]になった。 改善したけど、ほんのちょっと。うーむ。
1 これは間を飛ばした正味の変化である。途中ではメチルラジカル(CH3-)が触媒の様に働いて反応を進めるのだそうだ。
2 標準温度 298.15 [K] における振動と回転と並進の補正を含めているが、その寄与は小さいし、 両辺でほとんど同じなので燃焼熱への影響はさらに小さいから、含めなくても大きな問題はない。 実際の燃焼はもっと高い温度で起こるがその違いも無視できる。 定圧下の反応では温度が上昇すると気体は膨張して仕事をするので、それを考慮するために正しくはエンタルピーを使うが、 今回は温度を固定しているし、反応前後で分子の数が変わらないので、エネルギーで議論する。
3 これが物理学での標準。原子や分子のエネルギーは大幅にマイナスになる。 化学では、孤立原子のエネルギーを基準にしたり、単体で存在する分子のエネルギーを基準にする事が多い。
