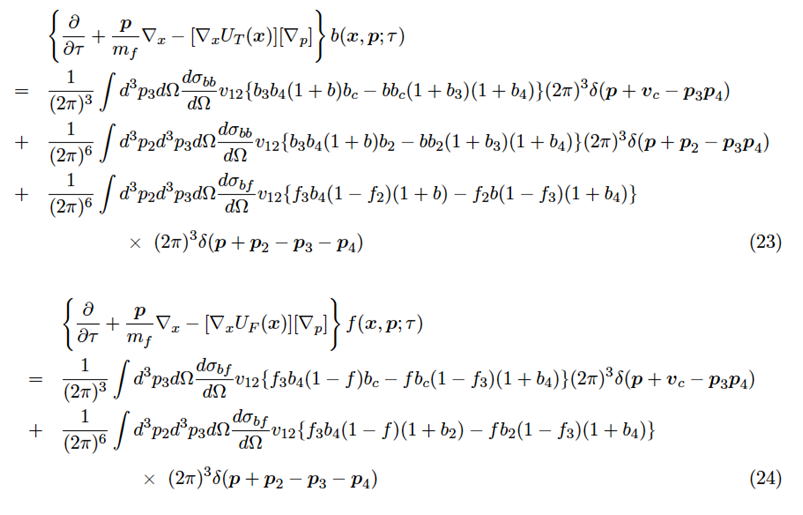研究テーマ:ボース・フェルミ混合気体の集団運動
目的
1) 異なる統計性を持つ二つの気体が混合したときのダイナミカルな性質
2) 気体の時間発展を記述する輸送理論の確立
系:温度ゼロ、ボソンは全てボース・アインシュタイン凝縮(BEC)状態
フェルミオンはフェルミ縮退
特徴 凝縮ボソン :全粒子が一つの1粒子状態を占有 単純な振動
フェルミ凝縮系:多くの1粒子状態を占有 様々な振動モードが混入する
計算方法:凝縮ボソン → Time-Dependent Gross-Pitaevskii (TDGP) Equation
フェルミオン → Vlasov Equation
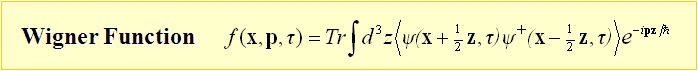
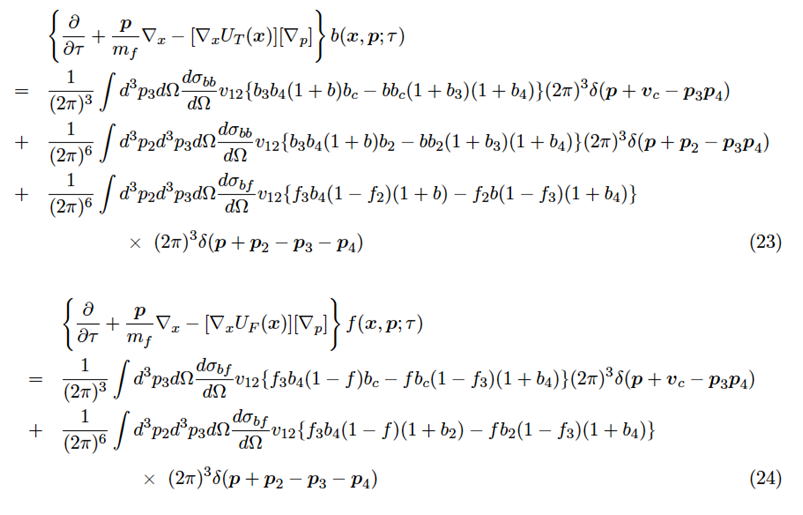
系を記述するハミルトニアン
基底状態 : 密度分布とボソンーフェルミオン相互作用
1) 単極子振動
”Monopole Oscillations and Dampings in Boson and Fermion Mixture
in the Time-Dependent Gross-Pitaevskii and Vlasov Equations”
T. Maruyama, H. Yabu and T. Suzuki, Phys. ReV. A72, 013609 (2005).
フェルミオン振動に線形応答理論では説明できない減衰が現れる。
2) 双極子振動
”Dipole oscillations in Bose-Fermi Mixtures in the time-dependent Gross-Pitaevskii
and Vlasov equations”
T. Maruyama and G.F. Bertsch, Phys. Rev. A77, #063611 (2008)
双極子振動で現れる、フェルミ振動の振る舞いを解析
Rb-Kの双極子振動の振る舞い
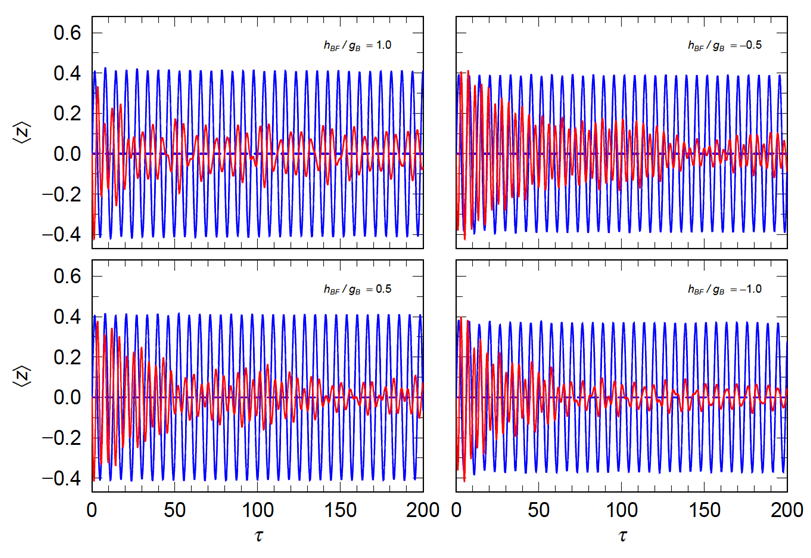
振動強度関数 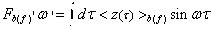
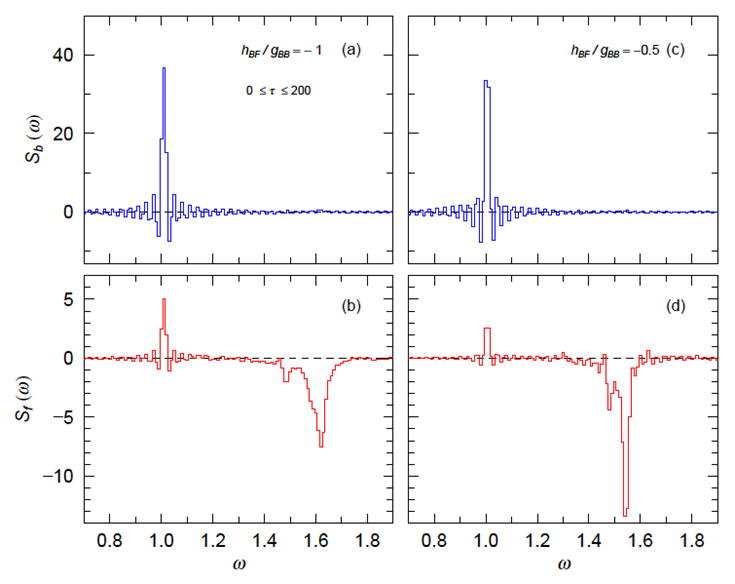
3) 四重極振動
”Quadrupole Oscillations in Bose-Fermi Mixtures of Ultracold Atomic Gases
made of Yb atoms
in the Time-Dependent Gross-Pitaevskii and Vlasov equations”
T.Maruyama and H.Yabu, Phys. Rev. A80, 043615 (2009), Virtual Journal of Atomic Quantum Fluids -- November 2009
京都大学高橋グループで実現された、Yb同位体を用いたボース・フェルミ混合気体の集団運動
B(10000) + F(1000) トラップ周波数 100×π[Hz]
| Yb-Ybの散乱長 |
| System |
aBB (nm) |
aBF (nm) |
aBB/aBF |
| 170Yb - 171Yb |
3.4533 |
1.9680 |
0.573 |
| 170Yb - 173Yb |
3.4533 |
-4.3730 |
-1.273 |
| 174Yb - 173Yb |
5.4630 |
7.2410 |
1.325 |
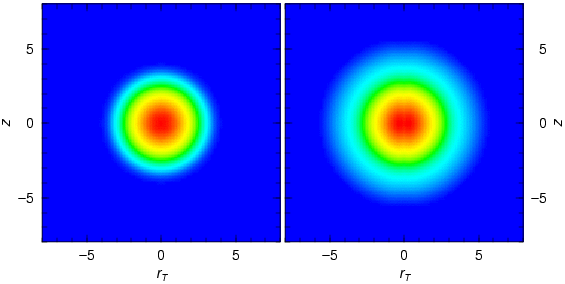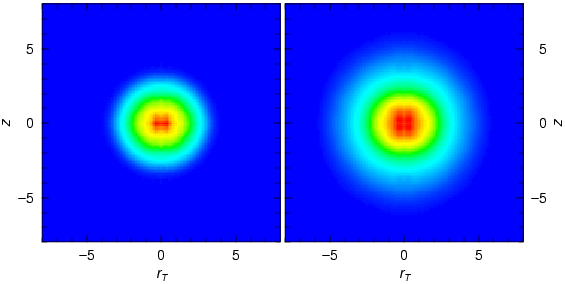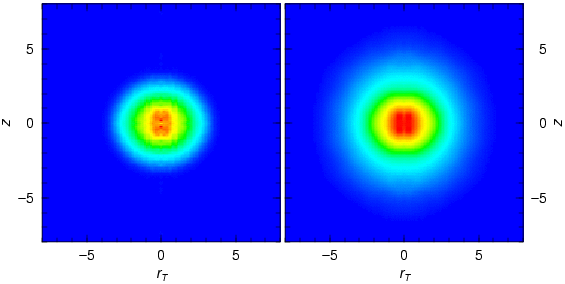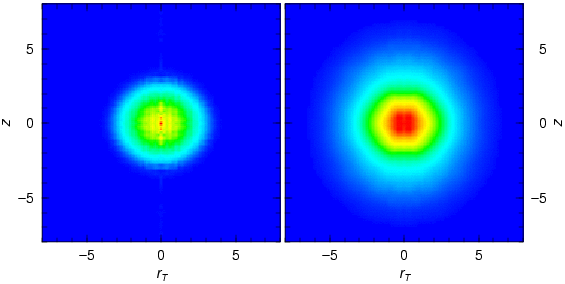
密度分布
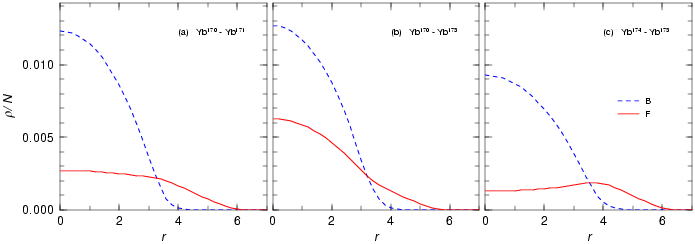
1) 170Yb - 171Yb
2) 170Yb - 173Yb
3) 174Yb - 173Yb